Обща процедура за оптимизация при една целева функция

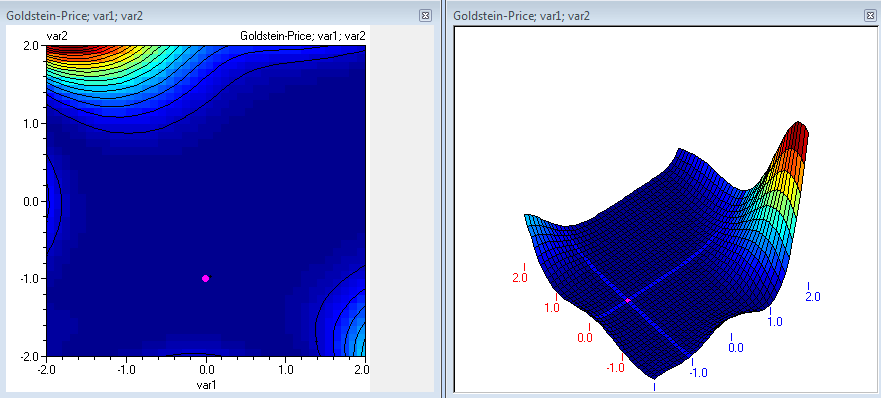
Използвайте Диаграми и методи/Оптимизация за да изберете модел за оптимизация. Оптимизацията може също да се стартира и от Контурни диаграми.Процедурата за оптимизация ще бъде описана на базата на модела на  Goldstein - Price който е даден във файл models.qsl. Функцията изглежда така (ако при изчертаването се получи еднаква стойност в целия диапазон, върнете се в таблицата, натиснете 'Преизчисли' и опитайте отново).

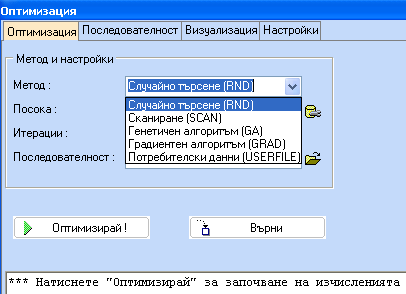
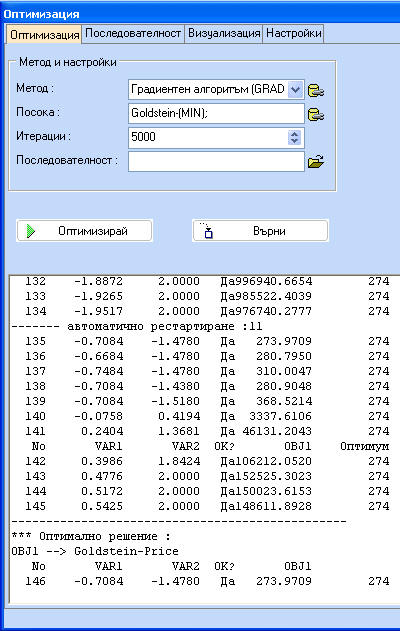
След като извикате програмата за Оптимизация, най напред трябва да изберете метод за оптимизация, брой на итерациите и посока на търсенето на оптимума. Някои методи като генетичните алгоритми и градиентните методи  имат допълнителни настройки, които са избрани по подразбиране с най-честоизползваните стойности.

Прозореца от дясната страна на фигурата по-долу дава допълнителни възможности за управление на процеса. Възможно е да се избере кои променливи трябва да се изменят по време на процеса и какви да са интервалите за изменението им. При задаването на горните и долните граници е възможно тези стойности да се установят за всички променливи като се кликне бутона "Всички".

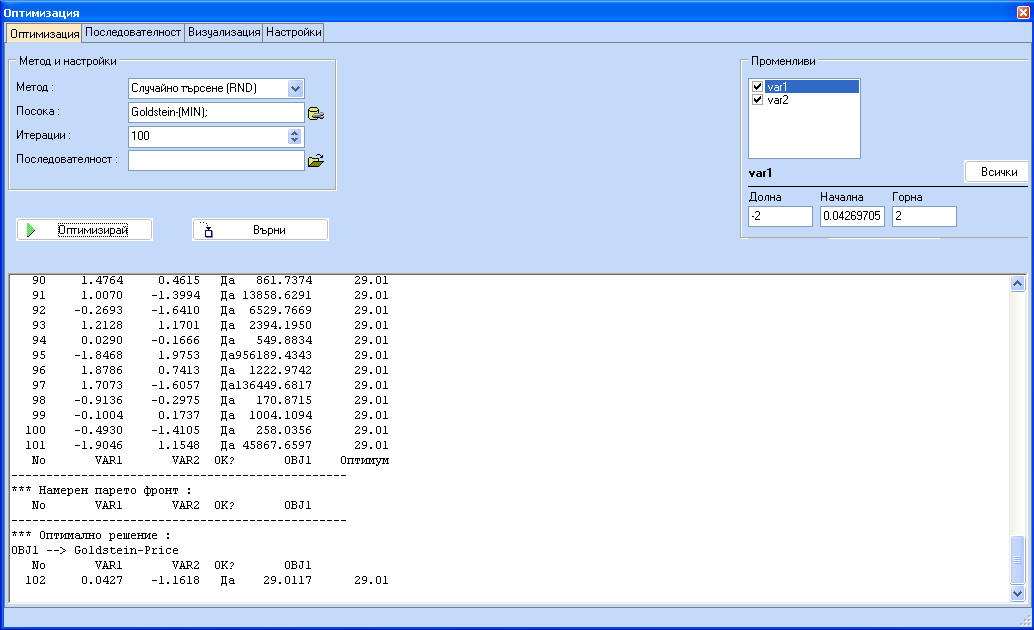
Кликнете бутона 'Оптимизирай' за да започнете оптимизацията. Ще се появява информация за всяка итерация. Първата колона показва номера на итерацията, следвана от променливите, ограниченията, допустимост и целевата функция. Последната колона е най-добрата стойност за първата целева функция, намерена до сега. След като процесът на оптимизация завърши е възможно да се види процеса на оптимизация чрез кликване на бутона "Оптимизация". Началната точка е отбелязана с кръстче, а крайната - с точка.

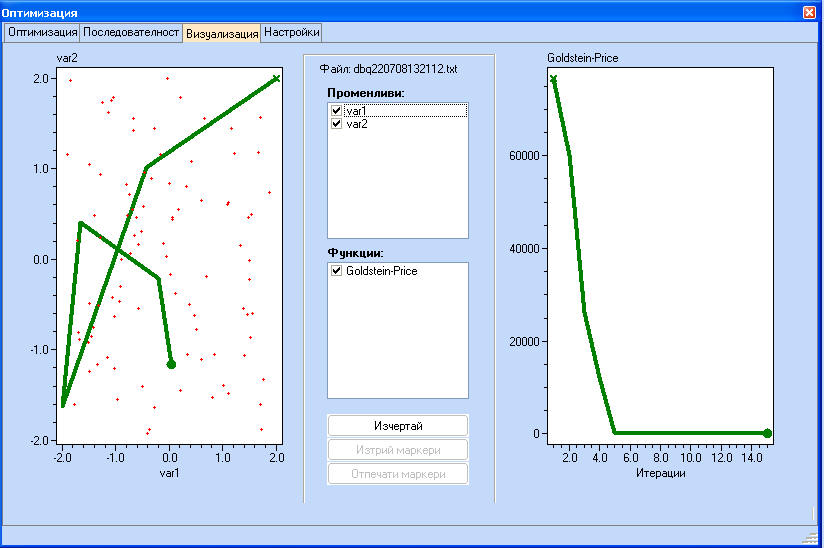
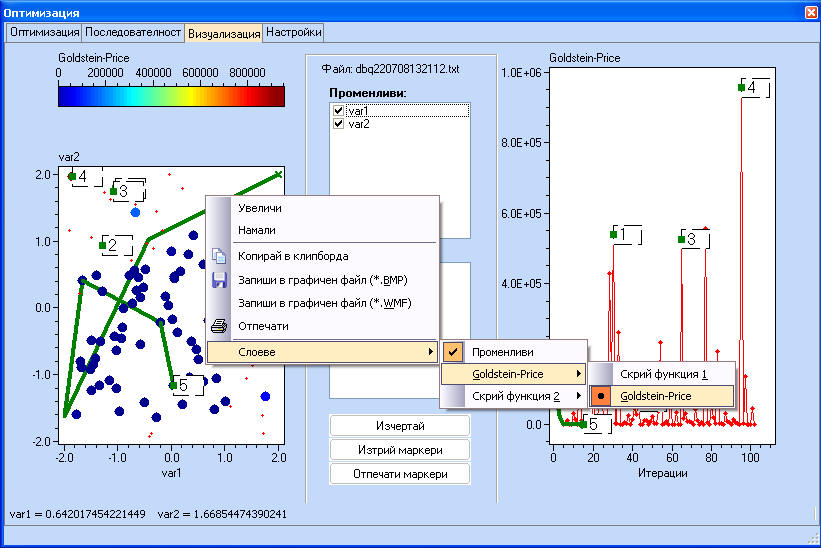
Ако след кликване на "Настройки" се махне маркировката на "Само оптимална следа - функция" можем да видим всички стойности на целевата функция.

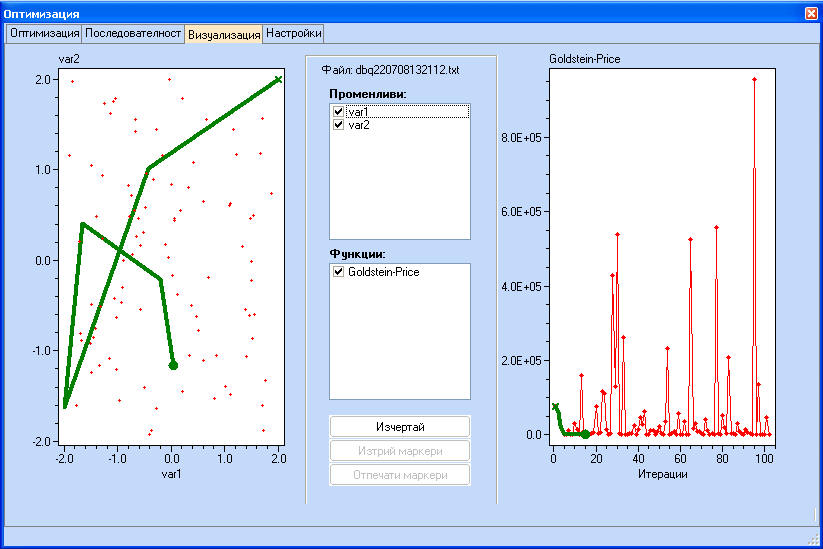
Като се натисне клавиша CTRL и се кликне върху която и да е от двете графики, потребителят може да постави визуални маркери. Ако маркерът е установен на лявата графика, той ще се появи и на дясната и обратно.  

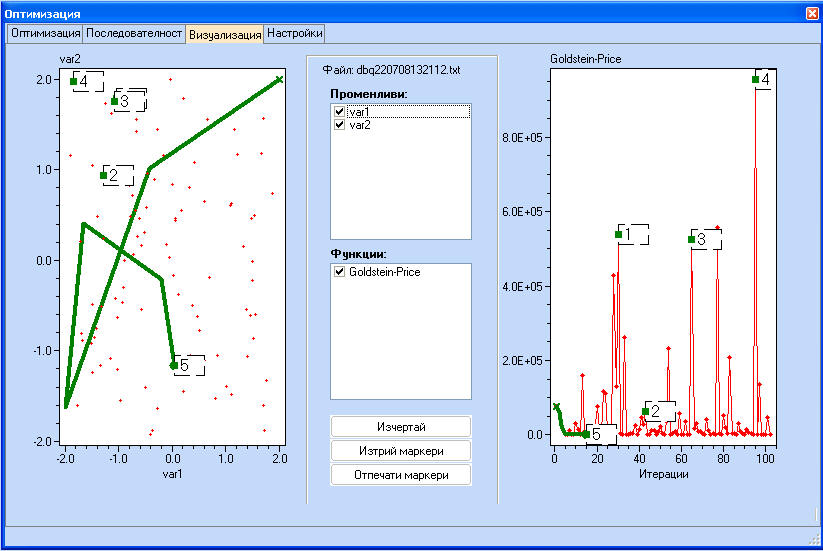
Стойностите на функцията, отбелязана с маркери се появяват в долната част на екрана с резултатите от оптимизацията.

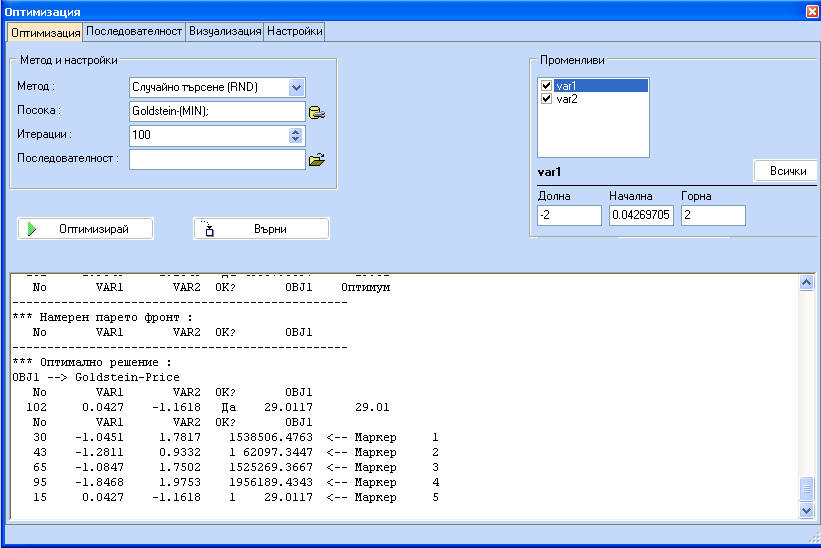
Двете графики могат да се увеличават или намаляват като се използва падащо меню (десен бутон върху графиката), при което се избира "Увеличи" или "Намали". На графиката с променливите е възможно да се покаже само разположението на точките на плана, а също и информация за стойността на функцията в прпизволно избрани точки, като се използва цветно кодиране.

След всеки цикъл на оптимизация е възможно да се сменят настройките и методите и да се повтори процедурата. Последната точка от предишната оптимизация ще стане начална точка на следващата.

С някои функции е ефективно и удобно да се комбинират няколко метода в последователност и следователно да се използват силните страни на всеки метод. Например, като се използва само градиентно търсене за функцията на Goldstein-Price при начални стойности на двете променливи var1=var2=-1, ще получим минимум равен на 274, (докато истинският минимум е 0). Причината за това е, че в близост до минимума функцията има много ниски стойности на градиента и следователно градиентното търсене спира.

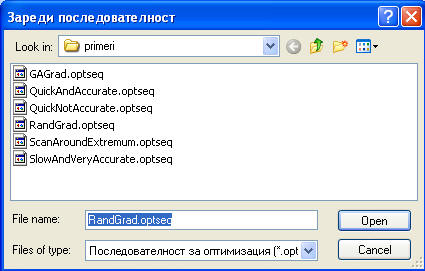
Има няколко предварително програмирани последователности в директорията с примерите. Файлът с последователностите трябва да се трябва да се избере в полето "Последователност". Изберете 'RandGrad.optseq' , която е една последователност от Случайно търсене, следвано от Градиентно търсене. С тази последователност, тръгвайки отново от var1=var2=-1 ще получим следното:

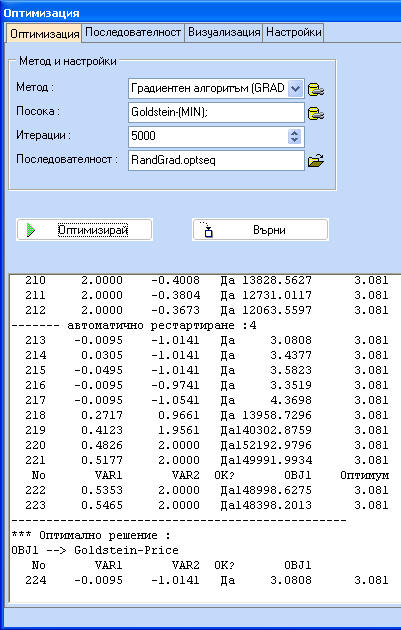
Вижда се, че комбинацията от двата метода дава резултат, който е много по-близко да истинския оптимум. Бутонът "Последователност" на фигурата по-долу дава възможност за създаване или редактиране на последователности. Всяка нова СТЪПКА копира настройките на предишната СТЪПКА и прилага зададените промени. Например в последователността RandGrad.optseq sequence е зададено, че първата стъпка се състои от случайно търсене (OMETHD=1) за 100 итерации и е последвана от Градиентен метод (OMETHD = 4) за максимум 5000 итерации.

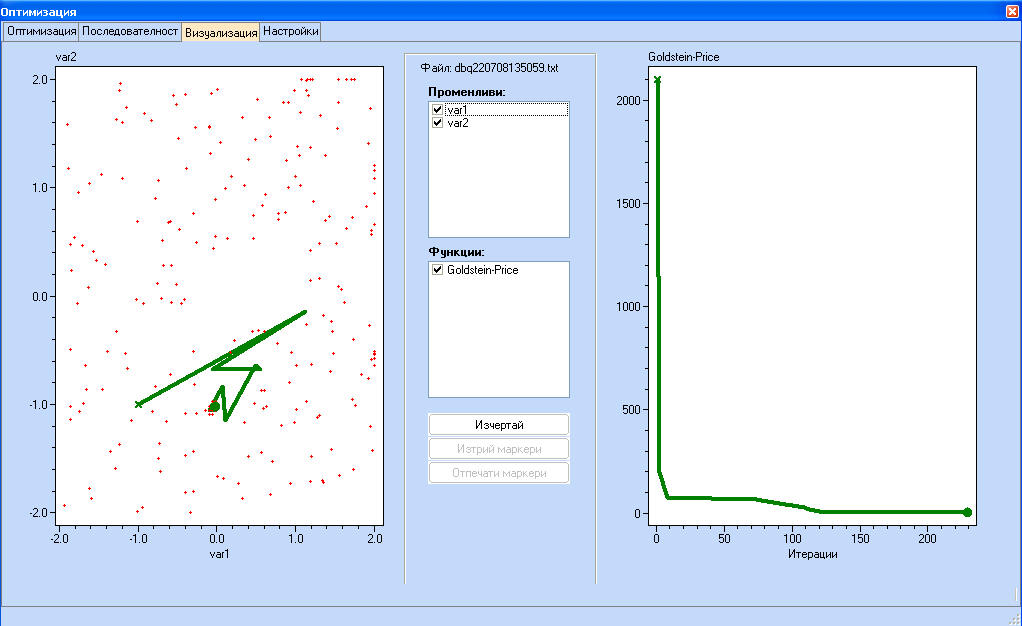
Във "Визуализация" се илюстрира пътекaта към оптимума. Може да се видят случайните точки и градиентното търсене около минимума. Това често е ефективна комбинация, тъй като случайното търсене може да идентифицира областта на оптимума, а градиентното търсене може да намери минимума по-точно като използва малък брой оценявания на функцията.

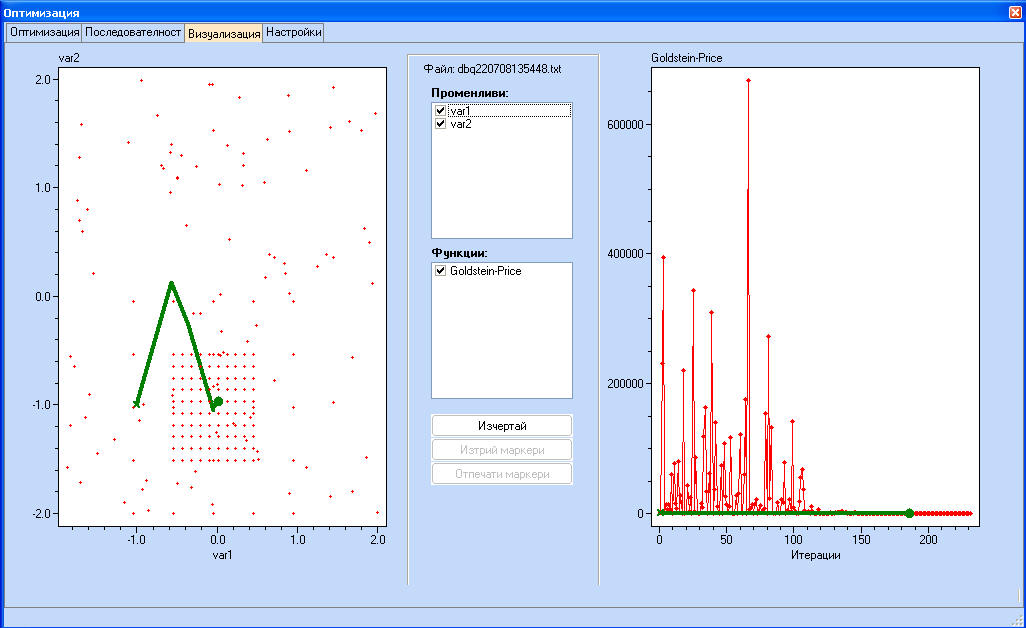
Последователността 'ScanAroundExtremum' представлява комбинация на две сканирания, като границите на променливите се стесняват около предварително намерения минимум.

Следва съдържанието на файла с последователността, използвана за построяване на графиките по-горе.

Следва пример за друга последователност: Quickandaccurate.optseq.

Файлът с последователността съдържа следните редове:

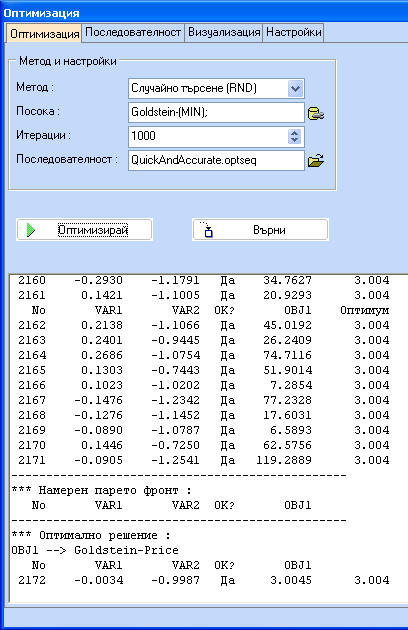
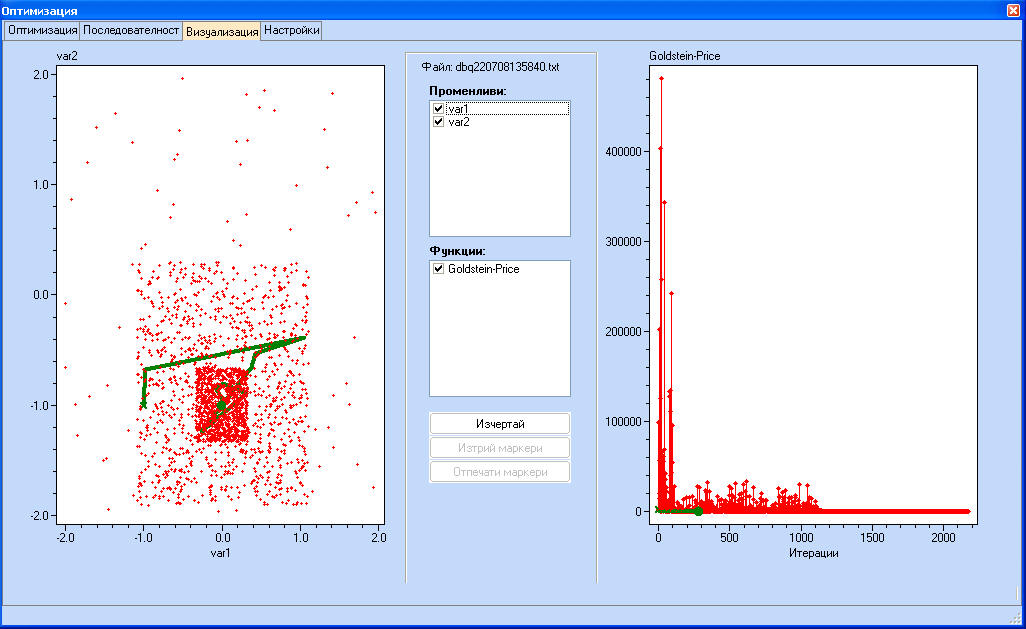
Започвайки със случаен план за 100 итерации, границите се намаляват с 55% от предишните - три пъти и сменяйки методи 1 и 2 - случайно търсене и сканиране. Вижда се, че глобалният оптимум е намерен с висока точност след 2171 итерации.

Виж също

• Многоцелева оптимизация

• Оптимизация с ограничения

• Упражнения по оптимизация, моделиране и робастно проектиране