Упражнения за съставяне на модели,
оптимизация и робастност
(файл OptimizationModels.qsl)
1. Изберете един от моделите и го пренесете в нова таблица. Озаглавете колоната и я обозначете от тип модел
2. Постройте контурни и 3Д-диаграми
3. Намерете екстремума опитайте различни методи и последователности. Опитайте да намерите екстремума с минимален брой итерации. Запишете най-доброто постижение координати на намерения екстремум, стойност на функцията и брой изчисления.
4. Съставете план на експеримент и постройте регресионен или кригинг модел. Можете ли да направите извод затова кой от двата подхода е по-подходящ за израбната функция?
5. Сравнете контурните диаграми построени по тези модели, с реалните. Ако има разлики, направете допълнителни експерименти за уточняване на модела. Къде е най-добре да направите новите експерименти? Ако функцията е описана с кригинг, използвайте функцията kriging_mse. Ако функцията е описана с регресионен модел опитайте да използвате Д-оптимални планове. Какъв е минималния брой опити, с които може да опишете функцията с модел?
6. Съствете стохастичен модел за средното и дисперсията. За регресионни модели от 2ри ред използвайте аналитичния подход. За всички останали модели използвайте Taylor2.
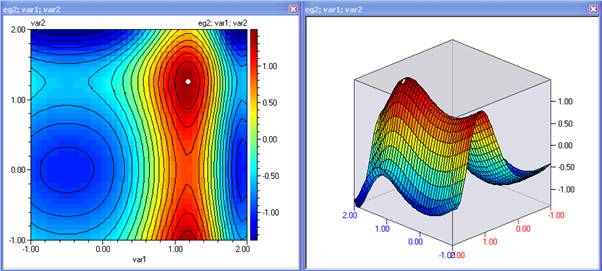
eg2
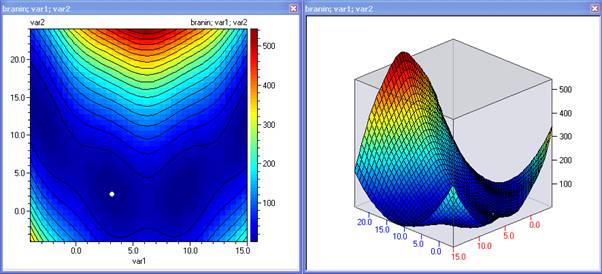
branin
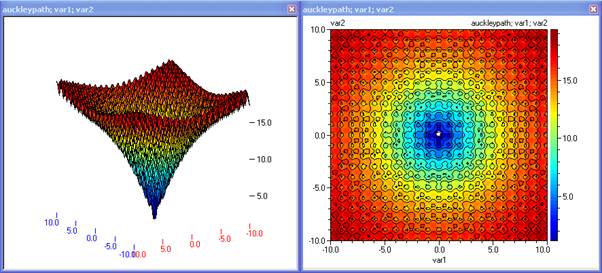
auckleypath
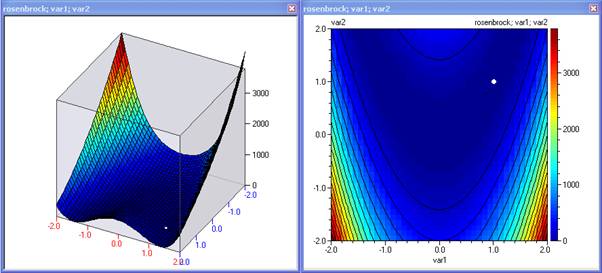
rosenbrock
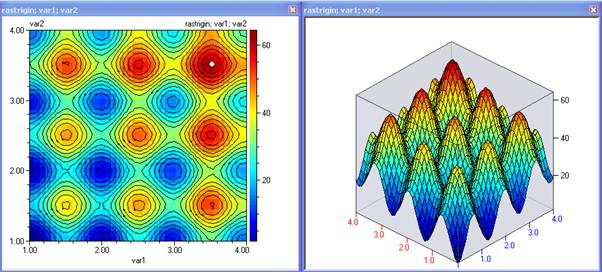
rastrigin
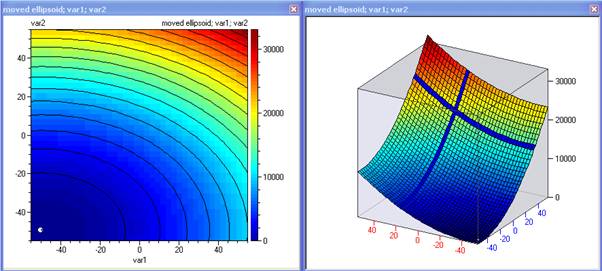
moved ellipsoid
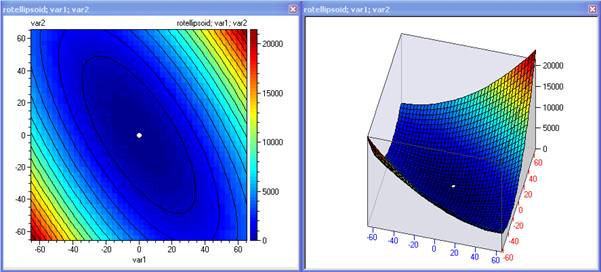
rotated ellipsoid
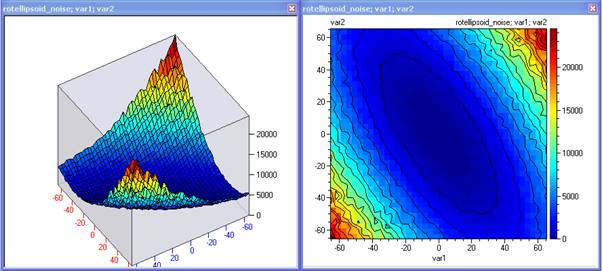
rotated ellipsoid с шум
Пример: Функция eg2
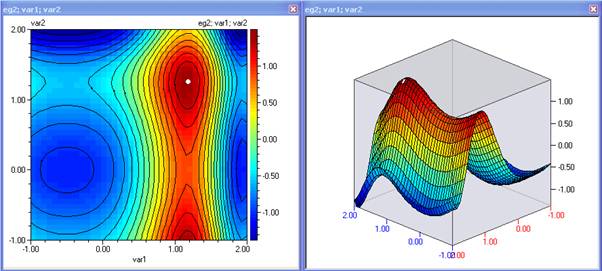
Контурни и 3Д диаграми и оптимизация
1. Отворете файл OptimizationModels.qsl и копирайте функцията eg2 в нова таблица:
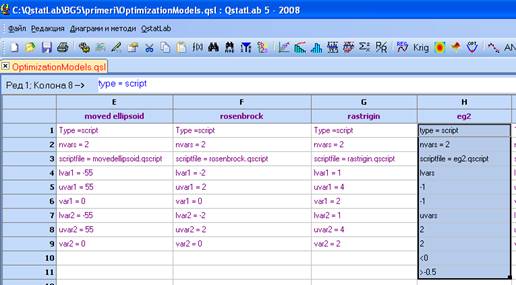
2. След като я нанесете в новата таблица, от Свойства на колоната въведете тип и име:
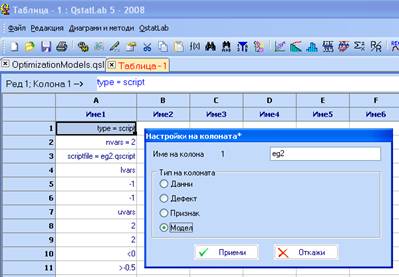
3. Затворете таблицата OptimizationModels и запишете новата таблица с име t1.qsl
4. Изчертайте контурни и 3Д диаграми Диаграми и методи/Контурни диаграми
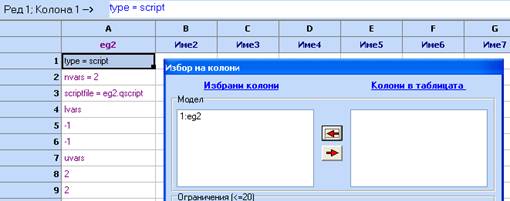
5. След получаване на диаграмата, използвайте бутона Оптимизация
6. Посочете, че желаете да намерите максимум
7. Натиснете Оптимизирай и след завършване на оптимизацията, можете да погледнете процеса в раздела Визуализация
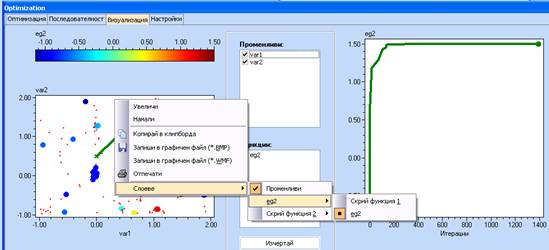
8. Използвайте бутона Върни в раздела Оптимизация, зада пренесете намерените резултати в контурните диаграми.
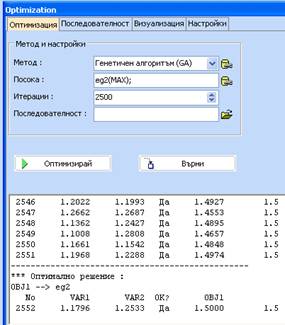
9. Маркирайте Нанеси тези резултати върху графиката и изберете бял цвят за оптимума. Натиснете Преизчертай.
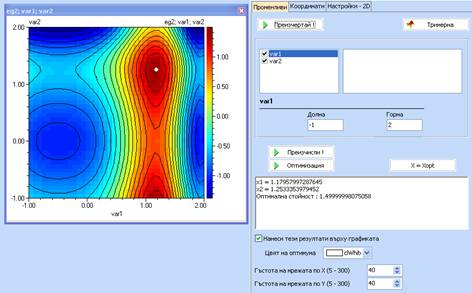
10. Повторете от т.4 като използвате различни оптимизационни методи и сравнете точността им и броя на изчисления. Отбележете, че направените изводите са валидни само за тази функция и резултатите от такива упражнения могат да бъдат коренно различни за други функции. Консултирайте се с преподавателите, в случай че имате съмнения относно изводите.
Построяване на модели
(продължение за примерна функция eg2)
1. Съставете план на експеримента. Диаграми и методи / Планиране на експеримента.
2. Като начало ще използваме пълен факторен експеримент с 3 нива. В полето Нива кликнете в първата таблица с десния бутон и изберете eg2.
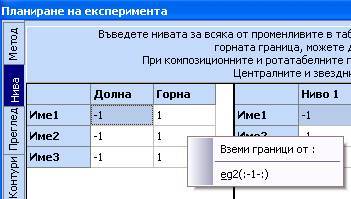
3. В таблицата Брой нива (ПФЕ) въведете 3 за двете променливи. Забележете че стойностите на нивата се променят автоматично. Възможно е нивата да се въведат и ръчно ако е необходимо неравномерно разпределение на техните стойности

4. В раздела Преглед, натиснете бутона Състави плана
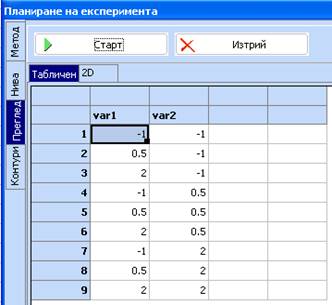
5. Използвайте бутона в таблицата ... зада пренесете получения план в таблицата:
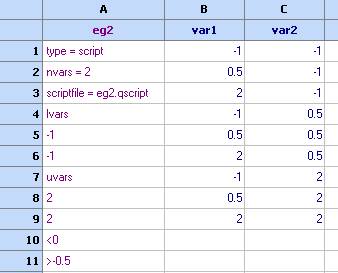
6. Изчислете стойностите на функцията в точките от този план. Използвайте модула оптимизация като въведете колоните по следния начин:
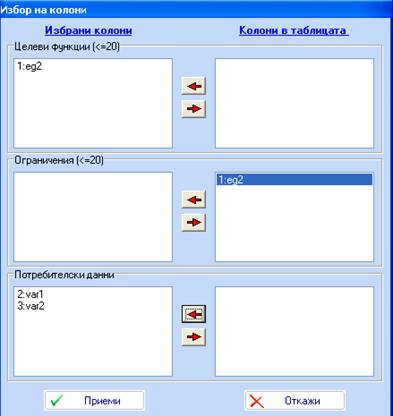
- Натиснете Приеми и след това Оптимизирай. Изплзвайте бутона В таблицата зада пренесете резултатите в таблицата и натиснете ОК
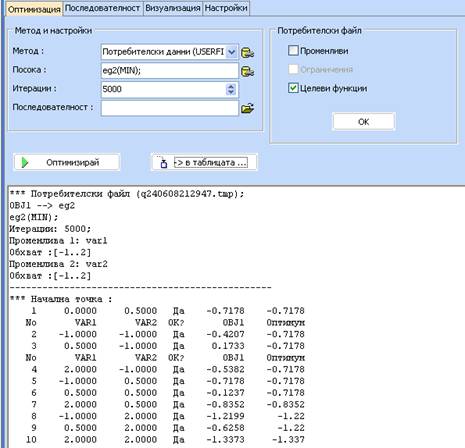
- Постройте кригинг модел (Диаграми и методи/Кригинг), като използвате var1 и var2 като входни величини и eg2 като изходна:
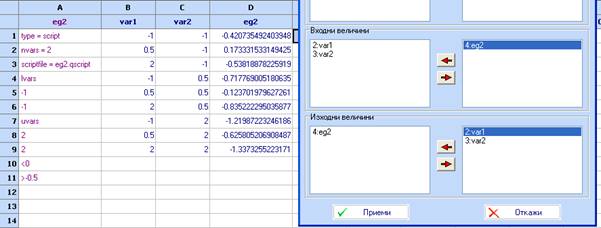
- Натиснете бутона изчисли и изчакайте процеса да привърши. Това ще разберете по това че зелената лента за показване на прогреса на изчисленията е изчезнала. По подразбиране са зададени 4 изчислителни цикъла.
- След като настройката привърши, използвайте бутона пренеси в таблицата зада копирате модела в таблицата. Ако кликнете този бутон с десен бутон на мишката ще можете да изберете кой модел да пренесете. След като направите избора, натиснете самия бутон с ляво кликване.
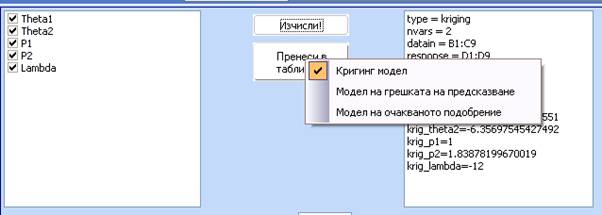
- Първоначално пренесете само модела на грешката на предсказване
- И постройте контурни и 3Д диаграми на грешката на предсказване. Ако те изглеждат така, това показва че е настъпила числена нестабилност, което се дължи на изроденост на матриците.
13. Зада избегнем това е необходимо да зададем по-висока долна граница на изменение на параметъра Lambda. За този пример -10 е гранична стойност, така че е по-добре да използвате -9.5. Натиснете Използвай тези стойности и след това Изчисли!.
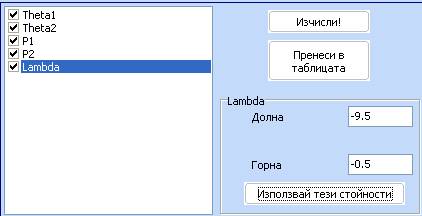
14. Отново пренесете модела на грешката в таблицата и се убедете че контурните диаграми сега изглеждат така:
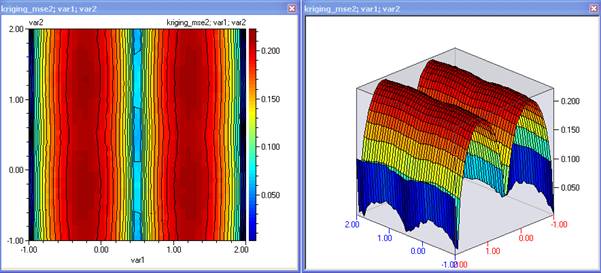
- Сега пренесете и останалите 2 модела (виж т.9). Забележете че трите модела се различават само по първия ред
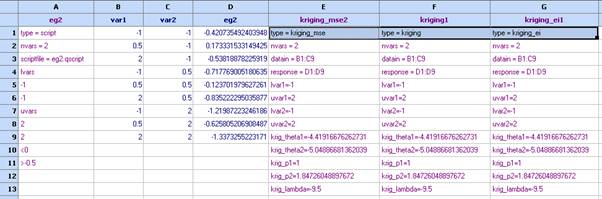
- Постройте контурни диаграми на модела kriging1. Това е модела който предсказва функцията eg2, в зададените точки.
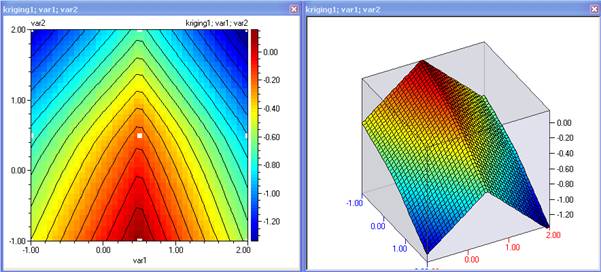
- Сравнявайки тези диаграми със истинските стойности на функцията показват, че моделът изобщо не е точен. При неизвестни функции може да не е възможно да се правят визуални сравнения (такъв е случаят в примера за аеродинамичния профил). В този случай се правят предсказания по точки които не са включени в модела и се сравняват разликите между предсказанията и измерените стойности. Процеса трябва да продължи докато грешките станат малки.
- Сега трябва да определим къде да проведем още експерименти зада извлечем най-полезна информация. Това може да се види от контурните диаграми на модела на грешката (Kriging_mse2). Там където грешката е максимална, е индикатор за недостатъчно информация. Със задържане на клавиша CTRL+кликване отбележете точките с най-висока грешка:
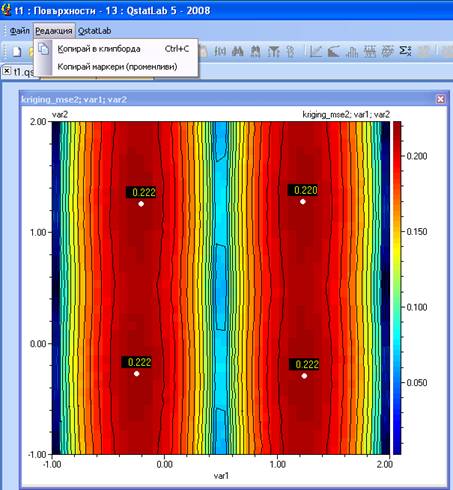
- Използвайте Редакция/Копирай маркери (променливи) и след това ги копирайте в таблицата под точките от плана на експеримента:
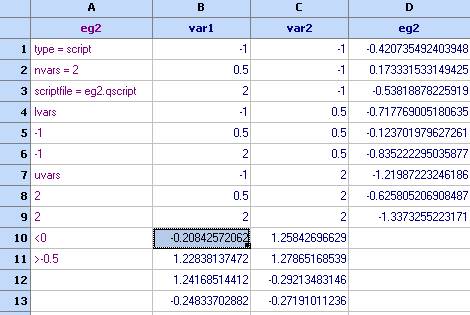
- В някои случаи е полезно да се проведат експерименти и там където функцията на очакваното подобрение е максимална. Затова повтаряме процеса за функция kriging_ei1
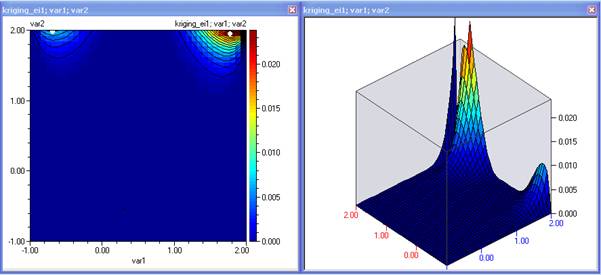
- Добавяме и тези точки към плана на експеримента.
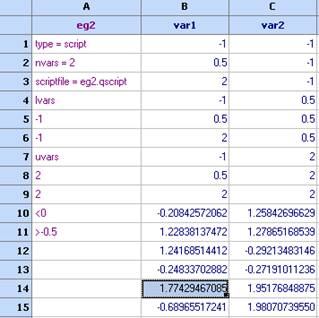
- Изчистете (не изтривайте) колоните със стойности на функцията и тези с кригинг моделите
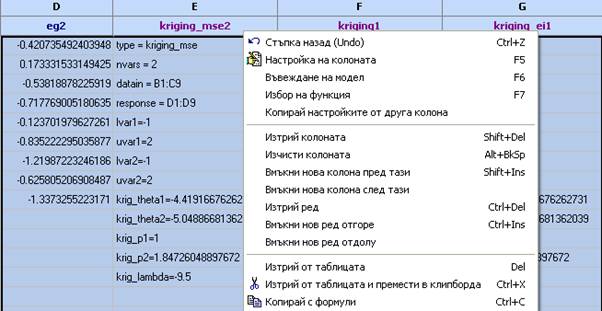
- Повторете процедурата от т.6.
- Продължете повторенията докато моделът отговаря на изискванията за точност, според целите за които ще се използва. На 2-ра итерация се получават следните резултати:
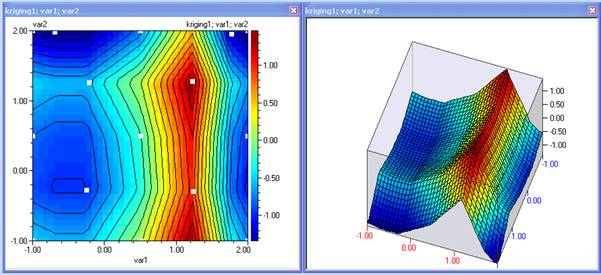
23. Виждаме че за целите за оптимизация този модел е достатъчно представителен, тъй като има проведени експерименти близо до показаните екстремуми, което означава че предсказанието на екстремумите е точно. Ако желаем да уточним модела още можем да проведем нови експерименти в максималните стойности на модела на грешката.
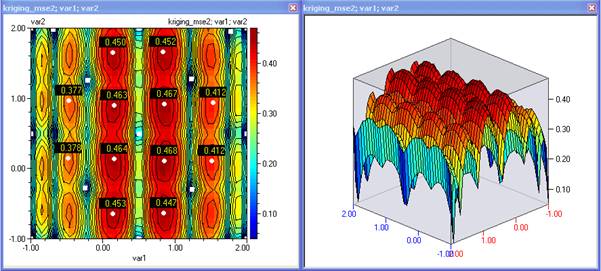
- Отбелязваме и пренасяме в таблицата под предишните точки. Функцията на очакваното подобрение сега има по-изразен максмум около минимума на целевата функция. Отбелязваме максмума и пренасяме:
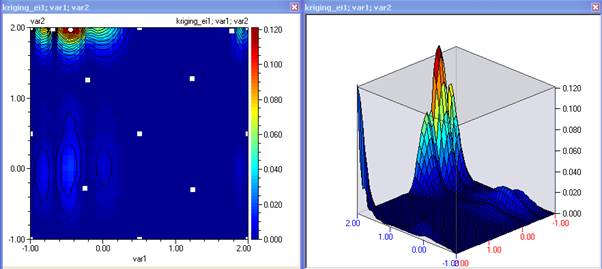
- Изчислете новите стойности на функцията и постройте нов кригинг модел. Постройте контури. На третата итерация модела изглежда така:
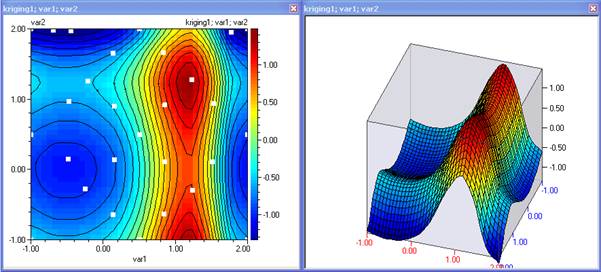
Този модел вече достатъчно прилича на този който се опитваме да моделираме и не са нужни повече итерации. Сега моделът е годен както за оптимизация, така и за предсказване. Регресионен модел от 4 ред, с горните данни изглежда така:
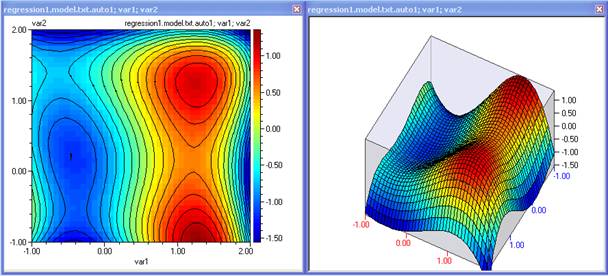
Интересно изследване може да се направи, ако след първоначалния план продължите с точки генерирани с Д-оптимален план, като сравнявате резултаите с този пример.
Робастност
(продължение за примерна функция eg2)
След като вече сме намерили достатъчно точен кригинг модел, можем да пристъпим към намиране на робастна оптимална стойност.
- Изчистете всички колони освен тези с данните и кригинг модела
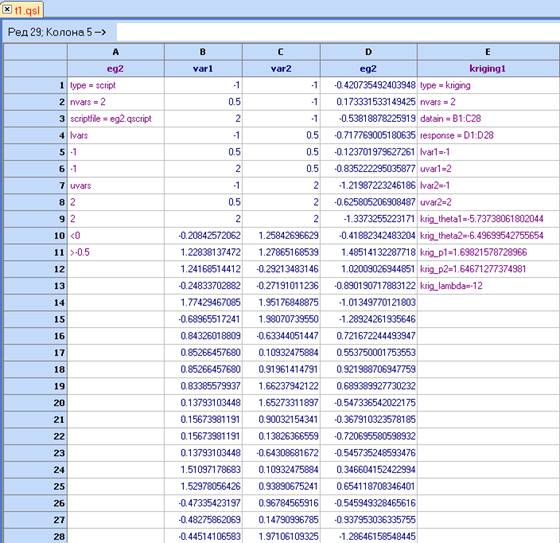
- ВАЖНО !!! Имайте предвид, че данните по които е построен кригинг модела са част от самия модел. Те се адресират в полетата datain и response. Предсказването по модела няма да работи, ако програмата не намери правилните данни в клетките указани в тези 2 полета.
- Ще създадем модели за средното и дисперсията. Кликнете в колона F и извикайте Редактор на модели. Попълнете полетата по следния начин:
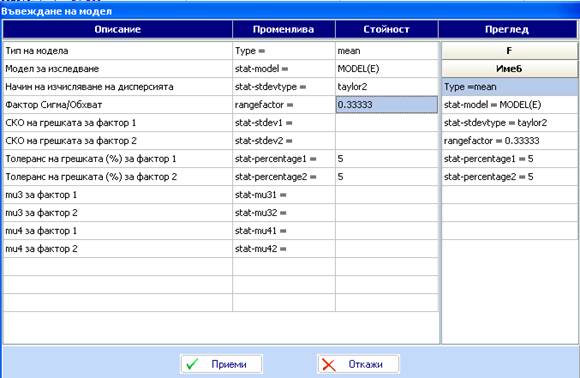
- Натинсете Приеми и моделът ще се появи в таблицата. Кликенете в колона G и повторете процедурата зада създадете модел на диспресията (variance). Променете имената на колоните (Настройки на колоната):
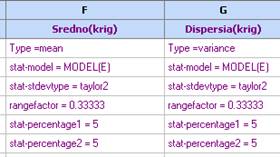
- Постройте контурни диаграми за средното и дисперсията. Оптималното робастно решение е там където дисперсията е минимална и стойността на средното е максимална. Това може да се намери с многоцелева оптимизация
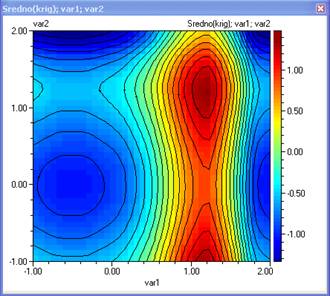
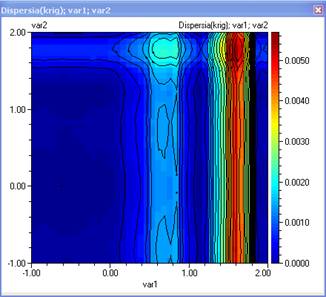
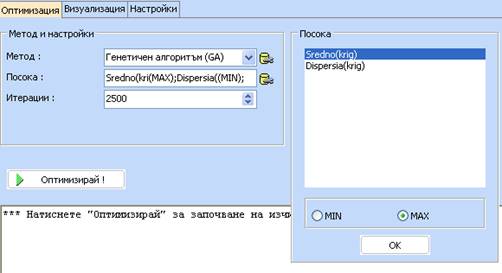
- Използвайте Диаграми и методи/Оптимизация:
- Укажете че ще търсите максимум на средното и натиснете Оптимизирай
- Виждаме че има няколко решения с ниска дисперсия. Маркираме това с най-високото средно
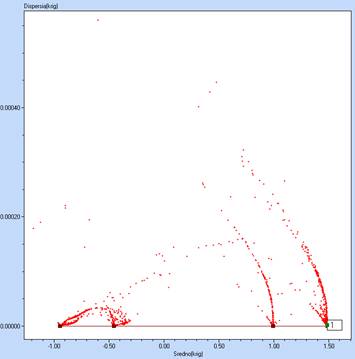
- Намирме че този маркер има следните координати (в раздела оптимизация)
No VAR1 VAR2 OK? OBJ1 OBJ2
1595 1.2017 1.2614 1 1.4893 0.0000 <-- Маркер 1
- Ако нанесем тези резултати графично ще видим че те изглеждат така:
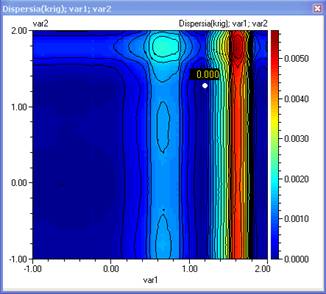
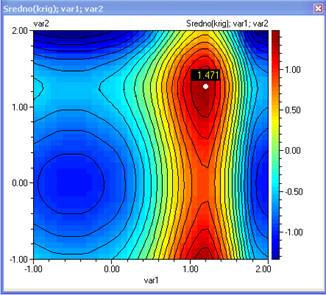
Резултатите потвърждават, че оптималното решение за тази функция е и робастно
Виж също:
Запъната греда - модел и оптимизация