Многоцелева оптимизация

Зaдачата е да се намерят Парето-оптимални решения за няколко (до 20 на брой) целеви функции, екстремумите на които са в ралични точки на пространството.

Да намерим множеството на оптималните решения за две функции, минимумите на които са в различни точки. Функциите, които ще разглеждаме са: завъртян елипсоид и преместен елипсоид. Те са записани в OptimizationModels.qsl. Всички участващи функции трябва да имат еднакъв брой променливи.Най-напред ще се приложат ограниченията за първата функция. Изберете иконката за Оптимизация ( ) и направете следния избор:

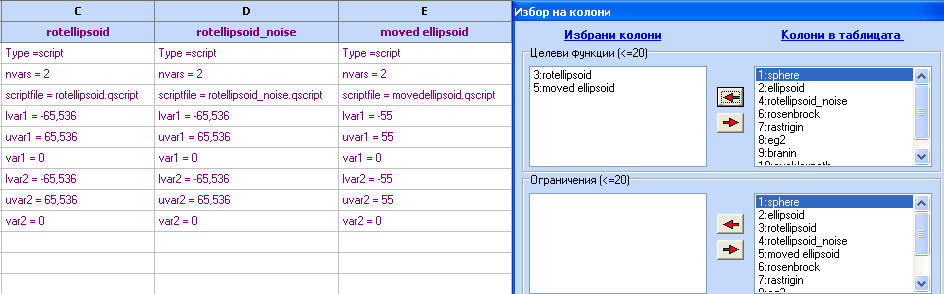
В момента генетичният алгоритъм е единственият, който може да се използва за Многоцелева оптимизация. Той се базира на алгоритъма NSGA2, който е разработен от Проф. Deb Kalmonoy.

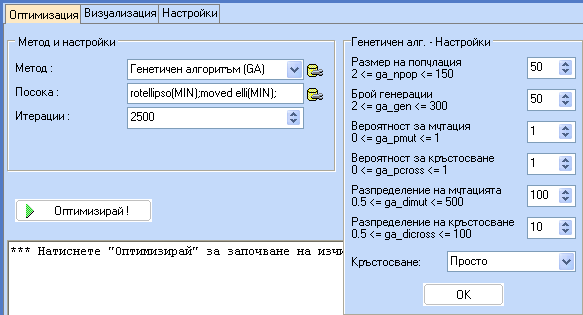
Кликнете 'Оптимизирай' и чакайте докато завърши оптимизацията. Когато това стане ще се появи т.н. "Парето фронт", който съдържа недоминираните решения - това са решения при които най-малко една целева функция е по-добра от останалите.

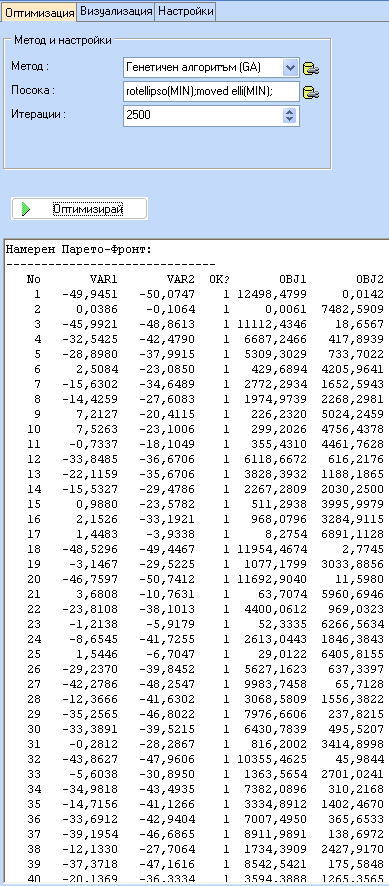
Броят на точките в Парето-фронта може да е между 1 и размера на популацията в генетичния алгоритъм. Парето фронта се визуализира с кафяви квадратни символи:

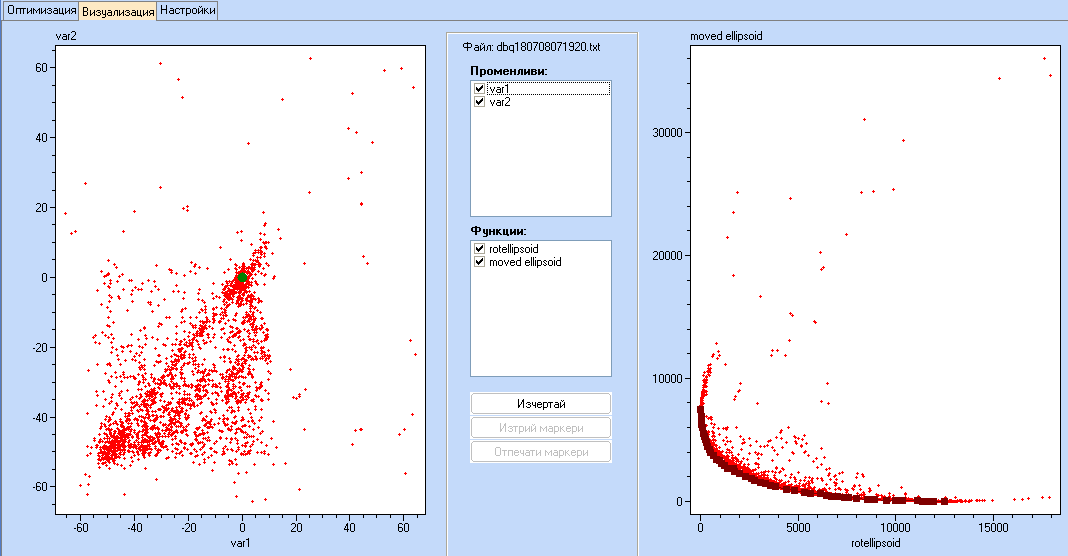
Парето фронта не дава едно единствено решение на оптимизационната задача, но дава възможност на потребителя да намери множество от потенциално оптимални решения. Като изучава Парето фронта, потребителят може да избере стойности на променливите, които съответстват на неговите нужди. Ако при натиснат клавиш  CTRL се кликне върху една точка, може да се избере маркер и да се види къде се намира тази точка в пространствата на 'променливите' и на 'целевите функции' .

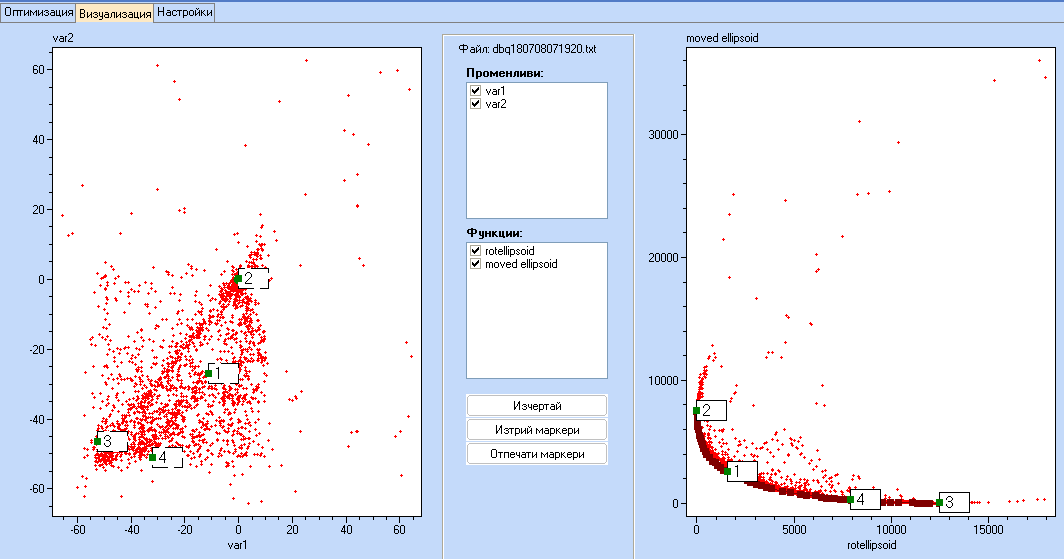
На екрана може да се види подробна информация за стойностите, съответстващи на всеки маркер:

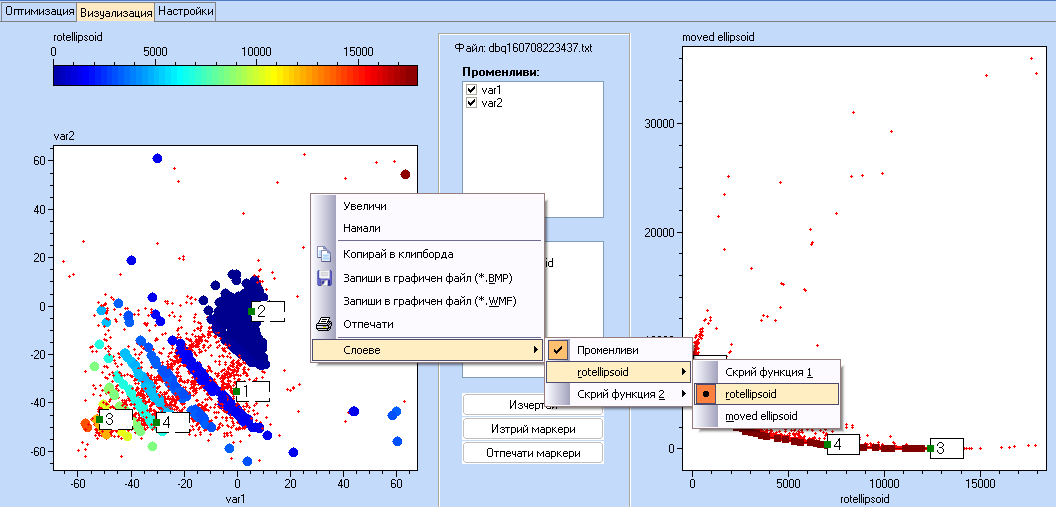
Тази методика е приложима за всякакъв брой целеви функции.

Виж също: