Реализация в QstatLab
QstatLab дава възможност за обучение и търсене на кригинг модели. Всъщност обучението е оптимизационна задача, където параметри за оптимизация са хипер параметрите Theta, P и Lambda (виж теория по-долу). За n променливи, трябва да се оптимизират 2*n+1 параметъра. Може да се види, че когато n нараства, броят на параметрите за оптимизация може да стане много голям, което да затрудни изчисленията. При задачи с голяма размерност се препоръчва да се поддържат постоянни и равни на 2 параметрите P.
Използването на кригинга се илюстрира с модела eg2, който е във файла OptimizationModels.qsl
1. Следвайте инструкцията в примера Оценяване на потребителските данни за да създадете следните входно-изходни данни:
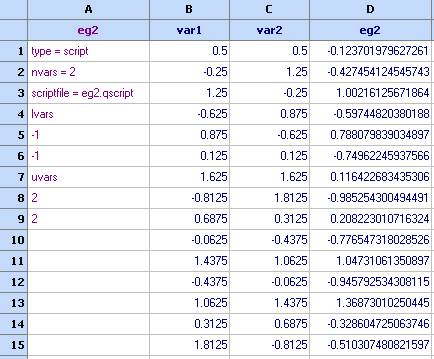
1. Изберете 'Кригинг' от менюто ‘Диаграми и методи’ и определете кои колони ще използвате. След това кликнете ‘Приеми’.
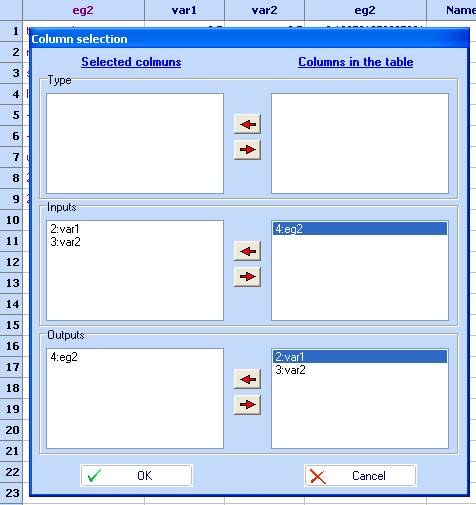
2. Появява се следният диалог за модула за кригинг:
· Хипер параметрите Тheta, P и Lambda се варират за да се максимизира CLF функцията (concentrated likelihood function).
· Избери параметрите с най-добра CLF след 4 изчислителни цикъла. Оптимизационният цикъл може да се повтори няколко пъти (4 в разглеждания случай). Ако оптимизационният алгоритъм намери различни оптимални стойности, модулът ще запази тези, които дават най-добра CLF.
· Максимален брой опити за настройка на параметрите: Когато има голям брой данни, процесът на настройка може да бъде бавен. Затова потребителят може да ограничи максималния брой точки, които се използват за настройка. Оригиналният брой данни ще се използват при предсказването.
· Повторни наблюдения. Когато има повторни наблюдения, потребителят може да избере да ги игнорира или да ги осредни.
· Посока на търсенето. Това е важно за изчисляване на функцията на очакваното подобрение, тъй като тя дефинира къде тя трябва да се ‘подобрява’. Ако не планирате да използвате функцията на очакваното подобрение, тогава игнорирайте тази настройка.
Кликнете ‘Изчисли!’ за да започнете процеса на настройки.
3. Процесът на настройки е завършен, когато изчезне индикаторът на прогреса. Ще се появи кратък анализ на модела:
Променливи: 2
var1
var2
Изходни величини: eg2
Настройка по 15 наблюдения от общо 15
------- Цикъл 1 -------
Hyper1 = 0.140839582095375
Hyper2 = -1.36944373360809
Hyper3 = 1.99999994728355
Hyper4 = 1
Hyper5 = -12
CLF = 15.653522767957
------- Цикъл 2 -------
Hyper1 = 0.120402574121496
Hyper2 = -1.44064427784928
Hyper3 = 1.99999347563375
Hyper4 = 1
Hyper5 = -12
CLF = 15.6626854699785
------- Цикъл 3 -------
Hyper1 = 0.14274766917893
Hyper2 = -1.41862247329643
Hyper3 = 1.99993653698941
Hyper4 = 1
Hyper5 = -12
CLF = 15.661620023147
------- Цикъл 4 -------
Hyper1 = 0.141607989379743
Hyper2 = -1.40568725289621
Hyper3 = 1.9998097109755
Hyper4 = 1
Hyper5 = -12
CLF = 15.6607562039429
измерена предсказана остатък грешка оч.подобрение
------------------------------------------------------------------------------------
-0.12370198 -0.12370197 -9.5405759E-9 3.265011E-7 1.2554041E-7
-0.42745412 -0.42745411 -1.303539E-8 4.4605398E-7 1.7150808E-7
1.0021613 1.0021611 1.2336649E-7 4.2216574E-6 1.7465999E-6
-0.5974482 -0.59744818 -2.0019345E-8 6.8477189E-7 2.6329152E-7
0.78807984 0.78807981 3.1233358E-8 1.0683336E-6 4.4200226E-7
-0.74962246 -0.74962245 -1.3482544E-8 4.6136943E-7 1.7739709E-7
0.11642268 0.11642268 4.8873919E-9 1.6716323E-7 6.9160677E-8
-0.9852543 -0.98525427 -3.3893017E-8 1.1596056E-6 4.4586676E-7
0.20822301 0.208223 6.0201221E-9 2.0600683E-7 8.5229984E-8
-0.77654732 -0.77654729 -3.0157146E-8 1.0314757E-6 3.9659655E-7
1.0473106 1.0473106 5.5662852E-8 1.9045944E-6 7.8797911E-7
-0.94579253 -0.94579254 8.4189272E-9 2.8811823E-7 1.1920107E-7
1.3687301 1.36873 6.5024793E-8 2.2246464E-6 9.20397E-7
-0.32860473 -0.3286047 -2.2139825E-8 7.5771561E-7 2.9134391E-7
-0.51030748 -0.51030742 -6.2123293E-8 2.1258001E-6 8.1737199E-7
Общ остатък 1.7579408004062E-7
Измерена – стойността от данните
Предсказана – стойността, изчислена от обучения кригинг модел
Остатък – разликата между Измерена и Предсказана
Грешка – корен квадратен от средноквадратичната грешка, изчислена в разглежданата точка като това наблюдение е махнато от множеството данни, използвани за предсказване
Оч. подобрение – вероятността за подобрение (по отношение на оптимума)
4. Получени са три модела:
Изберете всеки от тях и след това кликнете бутона ‘Пренеси в таблицата’. Моделите ще се пренесат в таблицата:
Моля обърнете внимание, че когато тези модели се използват, те ще се обръщат към данните, определени в полетата ‘datain’ и ‘reposnse’. Затова те трябва да са налице при изчисленията (моделите и данните да са в една и съща таблица).
Тези модели са готови за по-нататъшна оптимизация или начертаване на контурни диаграми. Контурите са следните:
Предсказване:
Грешка на предсказването – тази графика може да се използва за планиране на следващи експерименти там където грешката е най-голяма. Използвайте CTRL + кликване на мишката, за да поставите маркери на местата с максимална грешка и след това използвайте маркери Редактирай/Копирай (променливи) за да изкопирате координатите на маркираните точки. След това те могат да бъдат нанесени в таблицата.
Очаквано подобрение. То има максимум там където функцията на очакваното подобрение е максимална. Ако тя се използва за оптимизация, потребителят ще постави там най-малко един нов експеримент.
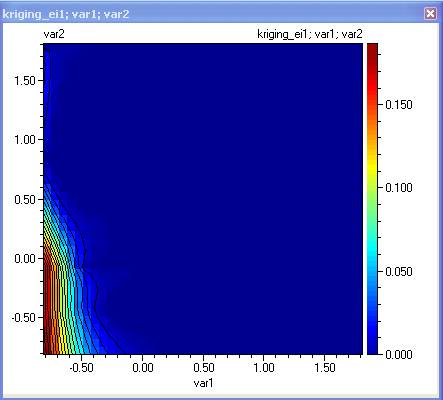
Кригинг модели могат да се дефинират и от Редактора на Модели:
Най-важните полета са nvars, datain, response. Забележете че полетата за Theta, P, Lambda са оставени празни. Пренесен в таблицата, модела изглежда така:
Всеки опит за използване на този модел, ще довете до автоматична настройка на параметрите, тъй като те не са зададени. Ако някой от кригинг параметрите е зададен, програмата ще използва зададените стойности и ще настройва останалите. Това може да се демонстрира например ако построим контурни диаграми за модел "Име 5"
Ако изберете 'Да', намерените кригинг параметри ще се запишат в модела, таблицата и това ще избегне автоматичната им настройка при бъдеща работа с този модел.
Контурната диаграма изглежда също както и по-горе
Виж също:
Упражнения по оптимизация, моделиране и робастно проектиране
Връзката между входовете x и наблюденията (отклиците) y се изразява като:
където 
представлява
функцията
или процеса,
който ще се
интерполира.
Ще оценяваме този отклик за комбинации от входовете, представляващи експерименталния ни план и ще използваме тази информация за построяване на апроксимация
Откликът в x се изразява като
където 
е
средното на
отклиците
при
различните
входове и 
е
Гаусова
случайна
функция с
нулево средно
и дисперсия 
.
Не
предполагаме,
че ε са
постоянни,
както е при
класическата
регресия, а
приемаме, че
тези грешки
са
корелирани.
Корелацията
между двете
точки е
свързана с
някаква
мярка за
разстояние
между двете
точки. В
случая се използва
следната
мярка за
разстояние:
където 
и 
са
хиперпараметри,
които
предстои да
бъдат
определени.
Корелацията
между
точките x(i) и x(j) се
дефинира
чрез
Допълнителен хиперпараметър е регуляризиращия член добавен към диагонала на R и означен като l:
където i = j.
Когато искаме да направим наблюдение в една нова точка x, формираме вектор на корелациите между новата точка и точките в които преди това сме провеждали наблюдения:
Ако x е близко до x(i), тогава тези точки са корелирани и предсказаният отклик ще се влияе силно от отклика в x(i). Обратно, ако точките са далече една от друга, корелацията е слаба и предсказаният отклик ще бъде слабо повлиян от отклика в x(i). Самото предсказване се дава от
,
където средното μ се дефинира от
Хипер
параметрите 
и 
,
както и l се
получават
чрез
максимизиране
на концентрираната
функция на
правдоподобието,
която е:
CLF =
,
а
дисперсията 
се
дава от
Друга полезна величина е средноквадратичната грешка на предсказването (MSE)
Тя ни дава мярка за точността на предсказване в x. Ако кригинг моделът се използва за оптимизация, може да се изчисли друга полезна величина, наречена ‘Очаквано подобрение’:
Виж също:
Упражнения по оптимизация, моделиране и робастно проектиране