Friction welding

 

Sources:

1. Barker, T, Clausing D. (1984). Quality engineering by design. The Taguchi method. The International QC forum. 11, No.8,28-52.
2. Vuchkov, I.N., Boyadjieva, L.N. (2001). Quality improvement with design of experiments. A response surface approach. Kluwer Academic Publishers, Dordrecht.

 

Methods:

Spreadsheet calculations, interpolations, Taguchi method, ANOVA, Regression analysis, Analytical models in robust engineering, Optimization, Contour plots, 3D plots.

 

Files: Friction welding – Loss function 1.qsl, Friction welding – Param design 2.qsl, Friction welding – Verification 3.qsl, Friction welding – Loss function 1.qsl, Friction welding – Tolerance design 4.qsl, Friction welding – Regression 5.qsl, Friction welding – Analytical - 6.qsl.

 

Short description of the problem:

 

Barker and Clausing (1984) used Taguchi method to find a welding system that reduces or prevents shaft breakage of the propeller in a high powered outboard engine. Performance characteristic y is the tensile strength. The target is to obtain y approximately equal to 160, while keeping standard deviation below 20. The factors are listed in Table 1. Denote by,  the values of factors measured in a physical scale. Their ranges are.

 

Barker and Clausing used a crossed array consisting of an  orthogonal array as a parameter design matrix (columns 2 to 7 of Table 2) and a  orthogonal array as a noise matrix. The total number of runs is . The variations of the process parameters within the tolerance limits shown in Table 1 are considered as noises. The  orthogonal array is conducted for each row of the parameter design. The levels of the noise factors in it are chosen equal to  and. For example, for the first run of Table 2 the first parameter is  which corresponds to  rpm. According to Table 2 the low cost tolerance of  is. Therefore, the levels of  in the  array for the first run of Table 2 are 900, 1000 and 1100 rpm.

 

 

TABLE 1. Factor levels, low cost tolerances and half

ranges of factor variations for the friction welding example.

 

Barker and Clausing do not display the full crossed array. They give only the parameter design and the tensile strength y, standard deviation of y, and signal-to-noise ratio. They are shown in Table 2. The data of Table 2 are given also in the file Friction welding – Param design.qsl.

 

TABLE 2. Parameter design, tensile strength, standard deviation and S/N ratio

 

A fragment of QSTATLAB spreadsheet for this example is shown below

 

 

1. Data analysis by Taguchi method (Barker & Clausing)

 

Loss function:

Barker & Clausing calculated Taguchi’s loss function :

 

,

 

where  is the target value for the strength. They estimated that a reduction of tensile strength by 60 incurs a loss of $ 500. Putting these values in L they obtained:

 

. Therefore:

 

 

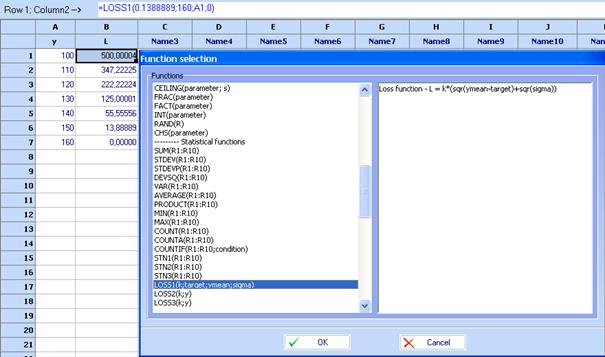
Let us calculate the loss function for strength values from 100 to 160, step 10. QstatLab has built-in functions for Taguchi’s loss functions. A function called LOSS1(k; target; ymean; sigma) calculates the following loss function:

 

.

 

We can use it to calculate  putting k = 0.1388889, target = 160, ymean =A1 and sigma = 0.

 

Click  and select LOSS1(k; target; ymean; sigma) and enter the above values for variables in the brackets. The value in cell B1 is 500.0004. Drag downward the point in the right bottom corner of cell B1 to obtain the other values of the loss function. The results are shown in column B of the spreadsheet below.

 

 

We can plot the loss function using “Interpolations” of QstatLab (). Select the columns as shown below:

 

 

Click OK to obtain the following diagram:

 

 

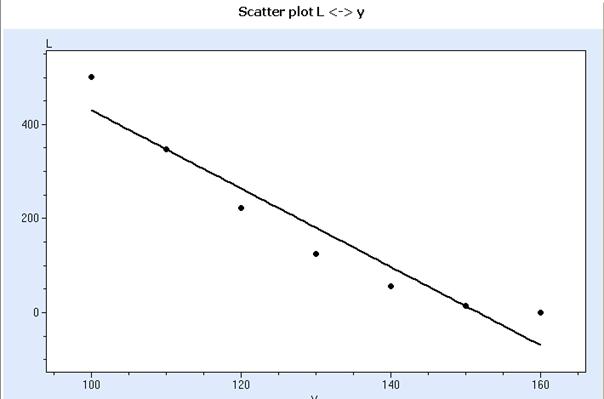
QSTATLAB uses by default linear regression for approximation of the data. It is clear that the linear approximation does not fit the data well enough. That is why click “Options → Diagram → Interpolation (L) → Type linear – y = a+bx” to open the following window:

 

 

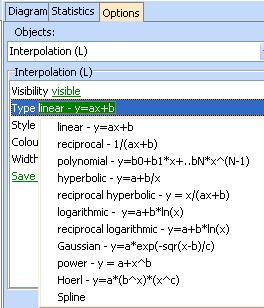
Select polynomial – y =b0+b1*x+…+bN*x^(N-1) and then choose “Polynomial order(L) = 2”:

 

Following plot will be obtained:

 

 

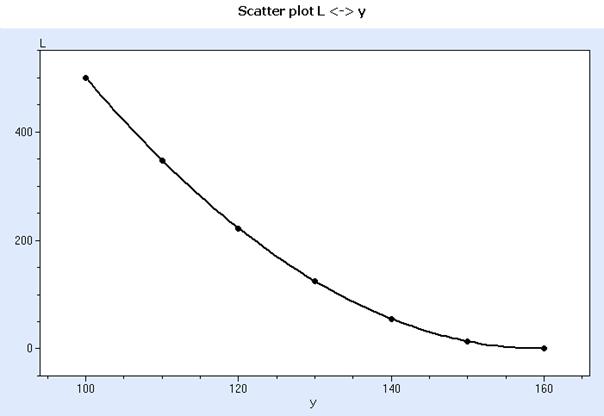
The statistical analysis shows very good approximation, which was expected:

 

General information for the data set y -L

-------------------------------------------------------------

Designated as X is y

Designated as Y is L

Number of elements:7

Average for X = 130,0000

Average for Y = 180,5556

Qx = 2800,0000

Qy = 210648,1819

Qxy = -23333,3352

Quality of fit = 1,0000

Trend line equation:     3556  -44,44*x+  0,1389*x^ 2

 

Statistical analysis and selection of parameter values by use of ANOVA:

 

Taguchi method makes conclusions on the basis of ANOVA results for mean values and signal-to-noise ratios. Consider first ANOVA for the tensile strength (file: Friction welding – Param design 2.qsl). Click  icon and select factors and tensile strength as is shown below:

 

 

Click OK to obtain following ANOVA table:

 

Analysis of Variance (ANOVA) for STRENGTH - (SPEED; HTPRS; UPPRS; LENGTH; HTTIME; UPTIME)

-------------------------------------------------------------------------

        Name                     Name     Levels     Levels

          x1                    SPEED          3     1000; 1200; 1400

          x2                    HTPRS          3     4000; 4400; 4800

          x3                    UPPRS          3     8500; 9000; 9500

          x4                   LENGTH          3     -30; 0; 30

          x5                   HTTIME          3     2,8; 3,2; 3,6

          x6                   UPTIME          3     3,2; 3,6; 4

-------------------------------------------------------------------------

      Source        Sums           DF    Variance        F           P

          x1   691,94296            2   345,97148     7,91359     0,00502

          x2  1248,33407            2   624,16704    14,27691     0,00042

          x3  1634,01407            2   817,00704    18,68785     0,00011

          x4   839,44296            2   419,72148     9,60052     0,00237

          x5   452,00519            2   226,00259     5,16948     0,02083

          x6   612,73407            2   306,36704     7,00770     0,00778

    Residual   612,06074           14    43,71862

-------------------------------------------------------------------------

       Total  6090,53407           26

Pooled Stdev = 6,61201      R-sq = 0,89951      R-sq (adj) = 0,81337

 

Confidence intervals for the mean, for each level

Confidence intervals are calculated on the basis of the standard deviation

for each factor level

 

     Level  Count      Mean    Variance        95% Confidence interval

SPEED

      1000      9 131,01111   228,14861     119,4007 <= 131,0111 <= 142,6215

      1200      9 141,74444   202,17278     130,8149 <= 141,7444 <= 152,6739

      1400      9 131,00000   244,50250     118,9807 <= 131,0000 <= 143,0193

HTPRS

      4000      9 126,25556   203,83278     115,2813 <= 126,2556 <= 137,2298

      4400      9 134,58889   118,24111     126,2305 <= 134,5889 <= 142,9473

      4800      9 142,91111   283,20111     129,9755 <= 142,9111 <= 155,8467

UPPRS

      8500      9 125,05556   174,37028     114,9053 <= 125,0556 <= 135,2058

      9000      9 134,58889   264,62611     122,0847 <= 134,5889 <= 147,0931

      9500      9 144,11111   118,06861     135,7588 <= 144,1111 <= 152,4634

LENGTH

       -30      9 127,00000   219,31500     115,6166 <= 127,0000 <= 138,3834

         0      9 140,24444   246,66028     128,1722 <= 140,2444 <= 152,3167

        30      9 136,51111   190,41111     125,9043 <= 136,5111 <= 147,1179

HTTIME

       2,8      9 129,56667   246,34750     117,5021 <= 129,5667 <= 141,6313

       3,2      9 134,60000   148,51500     125,2325 <= 134,6000 <= 143,9675

       3,6      9 139,58889   309,95361     126,0561 <= 139,5889 <= 153,1217

UPTIME

       3,2      9 131,22222   366,31444     116,5104 <= 131,2222 <= 145,9340

       3,6      9 141,32222    94,82944     133,8369 <= 141,3222 <= 148,8075

         4      9 131,21111   223,58111     119,7175 <= 131,2111 <= 142,7047

 

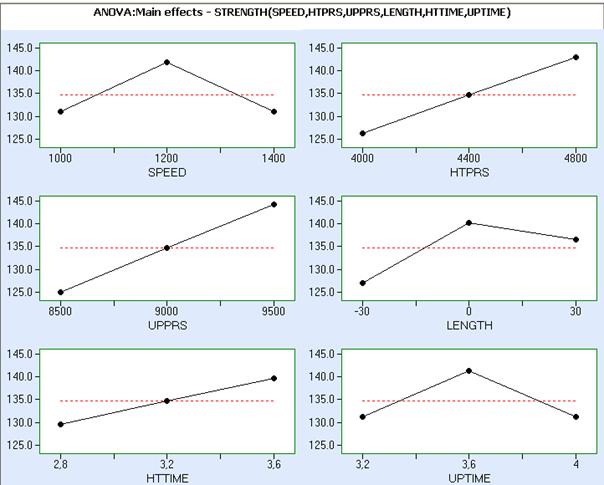
Main effects plots for tensile strength are shown below. The results of this analysis show that all factors are significant at significance level 0.05.

 

 

 

Consider now ANOVA results for S/N ratio. The corresponding ANOVA table is:

 

Analysis of Variance (ANOVA) for S/N - (SPEED; HTPRS; UPPRS; LENGTH; HTTIME; UPTIME)

-------------------------------------------------------------------------

        Name                     Name     Levels     Levels

          x1                    SPEED          3     1000; 1200; 1400

          x2                    HTPRS          3     4000; 4400; 4800

          x3                    UPPRS          3     8500; 9000; 9500

          x4                   LENGTH          3     -30; 0; 30

          x5                   HTTIME          3     2,8; 3,2; 3,6

          x6                   UPTIME          3     3,2; 3,6; 4

-------------------------------------------------------------------------

      Source        Sums           DF    Variance           F           P

          x1   132,32519            2    66,16259     2,68054     0,10337

          x2   165,83407            2    82,91704     3,35933     0,06432

          x3    79,33407            2    39,66704     1,60709     0,23534

          x4    74,03630            2    37,01815     1,49977     0,25694

          x5    24,89407            2    12,44704     0,50428     0,61450

          x6   736,44519            2   368,22259    14,91831     0,00034

    Residual   345,55630           14    24,68259

-------------------------------------------------------------------------

       Total  1558,42519           26

 

Pooled Stdev = 4,96816      R-sq = 0,77827      R-sq (adj) = 0,58821

 

 

Confidence intervals for the mean, for each level

Confidence intervals are calculated on the basis of the standard deviation

for each factor level

     Level  Count      Mean    Variance        95% Confidence interval

SPEED

      1000      9  33,15556    90,41778     25,8464 <= 33,1556 <= 40,4647

      1200      9  38,24444    11,41028     35,6480 <= 38,2444 <= 40,8409

      1400      9  34,07778    76,43444     27,3576 <= 34,0778 <= 40,7980

HTPRS

      4000      9  31,65556   129,06278     22,9230 <= 31,6556 <= 40,3881

      4400      9  36,83333    20,67500     33,3382 <= 36,8333 <= 40,3284

      4800      9  36,98889    24,33611     33,1969 <= 36,9889 <= 40,7809

UPPRS

      8500      9  32,75556    79,82278     25,8880 <= 32,7556 <= 39,6231

      9000      9  36,63333    20,79000     33,1285 <= 36,6333 <= 40,1382

      9500      9  36,08889    84,27361     29,0325 <= 36,0889 <= 43,1453

LENGTH

       -30      9  35,20000    19,62750     31,7946 <= 35,2000 <= 38,6054

         0      9  37,16667    24,34250     33,3742 <= 37,1667 <= 40,9591

        30      9  33,11111   141,57861     23,9650 <= 33,1111 <= 42,2572

HTTIME

       2,8      9  36,48889    16,74361     33,3436 <= 36,4889 <= 39,6342

       3,2      9  34,25556    93,96528     26,8044 <= 34,2556 <= 41,7067

       3,6      9  34,73333    80,98250     27,8161 <= 34,7333 <= 41,6506

UPTIME

       3,2      9  37,25556    10,23028     34,7970 <= 37,2556 <= 39,7141

       3,6      9  40,24444     0,91278     39,5101 <= 40,2444 <= 40,9788

         4      9  27,97778    91,60444     20,6208 <= 27,9778 <= 35,3347

 

ANOVA table shows that significant effects for the S/N ratio are UPTIME at significance level 0.05, SPEED and HTPRS at significance level 0.1.  The corresponding main effects plots are shown below:

 

 

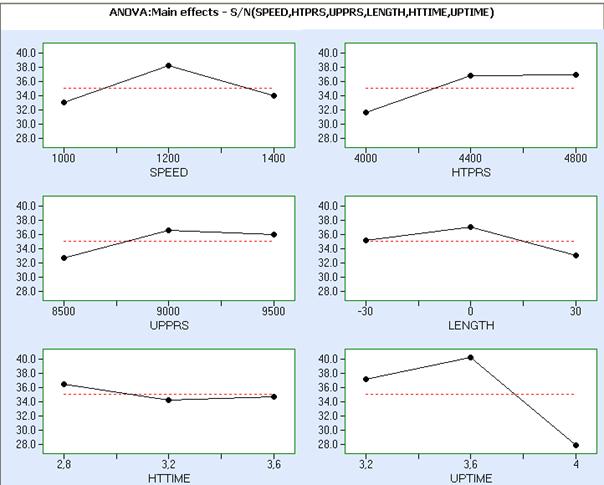
Barker & Clausing make following conclusions based on main effects graphs for the tensile strength and S/N ratio:

 

“Our analysis has shown that three of the factors have a significant effect on the S/N (“control”), while the other three only significantly effect the mean (”signal”) level. This is an advantage, since we can use the control factors to hold the variation to a proper level and move the mean with the signal factors. Our plots show us where to set the parameters. Speed is best at its mid-point of 1200 RPM. Heat pressure is best at 4800 psi. Upset pressure is a signal factor and is set to maximize the average strength at 9500 psi. Length is best at zero deviations from nominal.  Heat time gives the highest signal at 3.6 sec, even though the S/N is best at 2.8. Since this factor does not exhibit a statistically significant effect for S/N we move the level in favor of the mean response. The upset time is best set at the 3.6 or midpoint level.”

 

Tolerance design:

 

Barker & Clausing have performed a L18 tolerance design to verify the results obtained through parameter design analysis. In this design they use the optimal values found by parameter design and introducing noises according to the low cost tolerances, given in Table 1 (Friction welding – Verification 2.qsl):

 

 

 

SPEED: 1200  10%

HTPRS: 4800  15%

UPPRS: 9500  15%

LENGTH:     0  10%

HTTIME:   3.6  20%

UPTIME:   3.6  20%

 

The data are shown below:

 

 

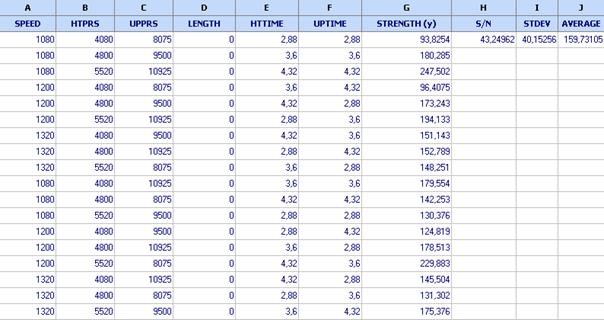
We calculate the signal-to-noise ratio using the built-in formula STN3(G1:G18). The formula for S/N ratio is:

 

.

 

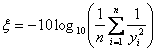The S/N ratio is 43.25. We also calculate the standard deviation by the formula: =STDEV(G1:G18). The result is STDEV = 40.15256. Vuchkov & Boyadjieva (2001) showed that this value is biased and the true value is about 50.

 

The average of the tensile strength in the verification experiment is calculated by the formula: =AVERAGE(G1:G18). The result is: 159,73105. The average strength is close to the desired, but the standard deviation is still too large. The loss is still too large: . In order to decrease the loss Barker & Clausing decrease the tolerances. They first calculate contributions of factors on the basis of ANOVA table of L18 noise array (file: Friction welding – Verification 3.qsl):

 

 

 

 

 

Analysis of Variance (ANOVA) for STRENGTH (y) - (SPEED; HTPRS; UPPRS; HTTIME; UPTIME)

-------------------------------------------------------------------------

        Name                     Name     Levels     Levels

          x1                    SPEED          3     1080; 1200; 1320

          x2                    HTPRS          3     4080; 4800; 5520

          x3                    UPPRS          3     10925; 8075; 9500

          x4                   HTTIME          3     2.88; 3.6; 4.32

          x5                   UPTIME          3     2.88; 3.6; 4.32

-------------------------------------------------------------------------

      Source        Sums           DF    Variance           F           P

          x1   774,44053            2   387,22027     1,01216     0,41105

          x2  9311,26356            2  4655,63178    12,16938     0,00527

          x3  5598,36737            2  2799,18368     7,31680     0,01927

          x4  5732,72390            2  2866,36195     7,49240     0,01821

          x5  3313,09952            2  1656,54976     4,33006     0,05971

    Residual  2677,98530            7   382,56933

-------------------------------------------------------------------------

       Total 27407,88018           17

 

Pooled Stdev = 19,55938      R-sq = 0,90229      R-sq (adj) = 0,76271

 

An approximate calculation of contributions is based on the sums of squares in ANOVA table and is shown below.

 

 

For example the contribution of the heat pressure to variability is:

 

 

Using this information they decided to decrease the tolerances of the factors as follows:

 

SPEED: 1200  10%    (no change)

HTPRS: 4800   5 %    (1/3 of the original)

UPPRS: 9500   7.5 % (1/2 of the original)

LENGTH:     0   10 %  (no change)

HTTIME:    3.6    5 %  (1/4 of the original)

UPTIME:    3.6    5 %  (1/4 of the original)

 

A new L18 design was carried out by Barker & Clausing to check the situation after the tolerance shrinking. The design is shown in the Table below (file: Friction welding – Tolerance design – 4)

 

 

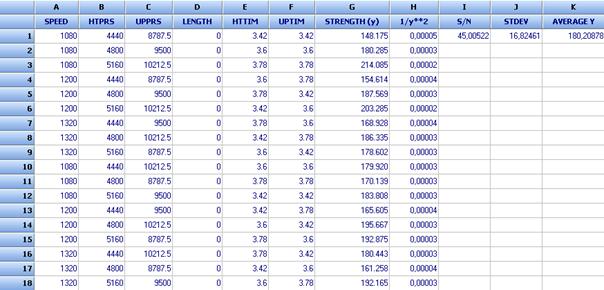
The calculation of S/N ratio, standard deviation and Average (y) has been done by use of the formulae given for the verification experiment.

 

One can see that after the tolerance design the standard deviation was reduced to 16.82 (before tolerance design it was 40.15). The average strength was increased to 180.21 (before 159.53).

 

Barker & Clausing reported average loss reduction from $ 350/engine to $ 22/engine. For 10000 engines this makes more than $ 3 million savings.

 

Conclusions:

 

• The experiment performed by Barker & Clausing made it possible to improve tensile strength to 180 and to decrease the standard deviation to 16.82.
• As a result the loss was decreased that made more than $ 3 million savings.
• To get these results Barker and Clausing have performed a parameter design with 27x18 = 486 runs, a verification experiment with 18 runs and a tolerance design with 18 runs. The total number of runs was 522.
• The optimal parameter values were found approximately, because in Taguchi method they are selected only amongst the parameter levels in the experiment.

 

2. Model-based approach to friction welding data

 

A model based approach to the same problem is possible (Vuchkov, Boyadjieva (2001). It reduces drastically the number of experiments and makes more reliable conclusions for the process than Taguchi method.

 

The model-based approach includes following steps:

 

• Development of a regression model
• Deriving analytically models of mean value and variance of the performance characteristic
• Minimization of variance while keeping the mean value on target, or minimization of loss function.

 

In the case of friction welding example we will use only 27 of 522 experiments to get the solution. The reduction of experiments is almost 20 times!

 

Building a regression model

 

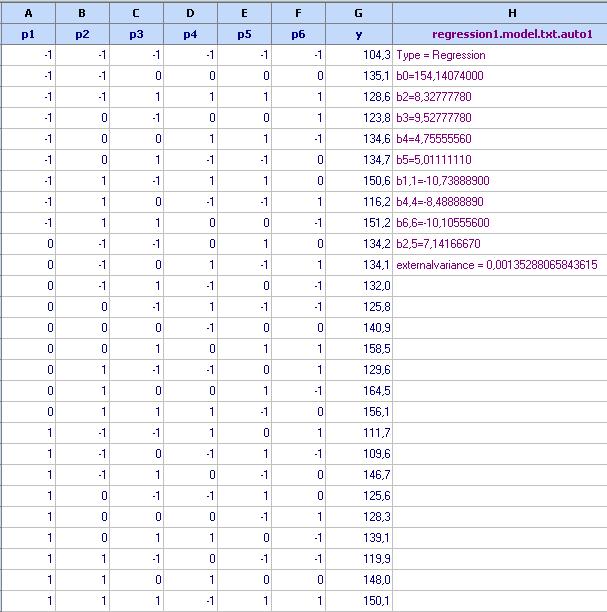
First we rewrite the parameter design in coded form (file: Friction welding – Regression – 5.qsl). Using the command = CODE(A1;1000;1400) and dragging downward we obtain the first column of coded design. The other columns of the parameter design matrix are coded in a similar way. A fragment of this matrix is shown below with the data for tensile strength (y). The full data are in file Friction welding-Regression-5.qsl. It contains also a model obtained at the end of calculations.

 

 

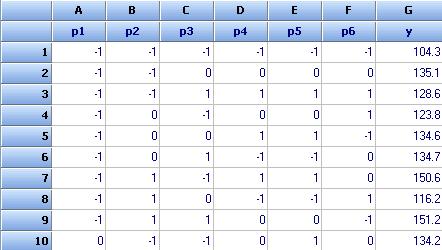
We want to create a second order regression model for the tensile strength. We will use Regression analysis ().We start with column selection as follows:

 

 

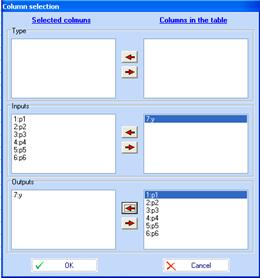
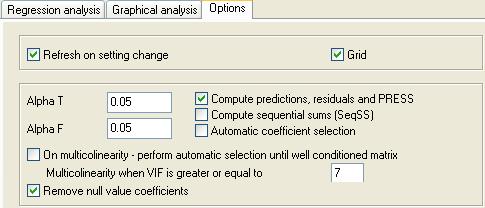
In this example the number of unknown coefficients in a second order polynomial with 6 factors is 28, while the number of runs in parameter design is only 27. That means that information matrix is ill conditioned (there is multicolinearity). Any regression analysis program is unstable under such circumstances. QstatLab can remove some terms so that to avoid multicolinearity. First we check if there are some null value coefficients. To use this option we should set the regression analysis properties as follows:

 

 

Click  and select second order model:

 

 

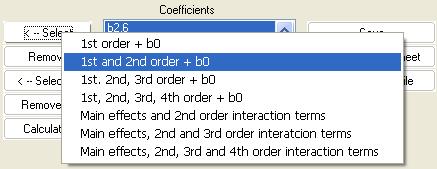
Choosing full second order model we obtain the following:

 

*** Number of coeffieicnets ( 28) should not be greater than the number of data ( 27)

Results:

*** Ill conditioned matrix (norm: 5200503981,56435) => results might be inaccurate

*** Coefficient b4,6  has a null value and has been excluded from the model.

*** Coefficient b3,6  has a null value and has been excluded from the model.

*** Coefficient b3,5  has a null value and has been excluded from the model.

*** Coefficient b1,5  has a null value and has been excluded from the model.

*** Coefficient b1,2  has a null value and has been excluded from the model.

*** Coefficient b2,6  has a null value and has been excluded from the model.

---------------------------------------------------------------------------

Observations: 27

Input variables: 6

Number of coefficients: 22

Assignments:

      x1 <--> p1

      x2 <--> p2

      x3 <--> p3

      x4 <--> p4

      x5 <--> p5

      x6 <--> p6

      y <--> y

---------------------------------------------------------------------------

y = 154.157-0.015x1+8.328x2+9.528x3+4.756x4+5.010x5-0.017x6-10.729x1x1-0.006x2x2+0.006x3x3-8.489x4x4-0.023x5x5

-10.117x6x6+0.002x2x3-0.016x3x4-0.020x4x5-0.011x5x6+0.022x1x3-0.002x1x4+0.020x1x6-0.022x2x4+7.117x2x5

---------------------------------------------------------------------------

 

Many of regression coefficients are close to zero. To select only significant coefficients we click  and select the Effects half normal plot as follows:

 

 

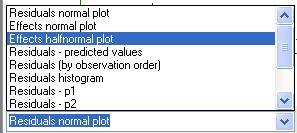
The obtained half normal plot of thr effects is:

 

 

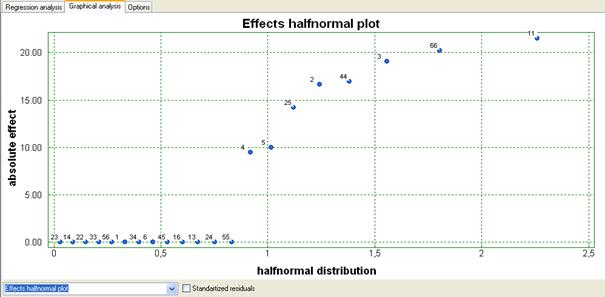
We can delete from the model all terms that are close to zero. Removing all terms with coefficients close to zero we obtain following model:

 

y = 154.141+8.328x2+9.528x3+4.756x4+5.011x5-10.739x1x1-8.489x4x4-10.106x6x6+7.142x2x5

---------------------------------------------------------------------------

  Regressor       Coef    St. Dev          t          p      Signif    VIF

         0     154,141      0,019   8230,393      0,000       +

         2       8,328      0,009    960,585      0,000       +      1,000

         3       9,528      0,009   1099,001      0,000       +      1,000

         4       4,756      0,009    548,539      0,000       +      1,000

         5       5,011      0,009    578,017      0,000       +      1,000

        11     -10,739      0,015   -715,163      0,000       +      1,000

        44      -8,489      0,015   -565,323      0,000       +      1,000

        66     -10,106      0,015   -672,986      0,000       +      1,000

        25       7,142      0,011    672,606      0,000       +      1,000

    Significance test was performed at level = 0,05

---------------------------------------------------------------------------

                                 ANOVA                                                

---------------------------------------------------------------------------

        Source      Sqr. sum       DOF    Variance           F         P

        Model     6090,50972      8      761,31372   562735,30886   0,00000

      Residual        0,02435     18       0,00135

         Total     6090,53407     26

--------------------------------------------------------------------------

                                   PRESS                                        

---------------------------------------------------------------------------

   N          y          yp        y-yp    PRESS(i)    SE pred.St. residual

   1     104,3000   104,3269    -0,0269    -0,0446     0,0232    -0,9410

   2     135,1000   135,0741     0,0259     0,0350     0,0187     0,8190

   3     128,6000   128,6324    -0,0324    -0,0538     0,0232    -1,1357

   4     123,8000   123,7685     0,0315     0,0395     0,0166     0,9592

   5     134,6000   134,5741     0,0259     0,0326     0,0166     0,7899

   6     134,7000   134,6741     0,0259     0,0378     0,0206     0,8515

   7     150,6000   150,6213    -0,0213    -0,0390     0,0248    -0,7834

   8     116,2000   116,2269    -0,0269    -0,0408     0,0215    -0,9004

   9     151,2000   151,1519     0,0481     0,0650     0,0187     1,5210

  10     134,2000   134,1546     0,0454     0,0925     0,0262     1,7608

  11     134,1000   134,1046    -0,0046    -0,0077     0,0232    -0,1622

  12     132,0000   131,9907     0,0093     0,0135     0,0206     0,3041

  13     125,8000   125,7630     0,0370     0,0541     0,0206     1,2165

  14     140,9000   140,8963     0,0037     0,0050     0,0187     0,1170

  15   R 158,5000   158,5741    -0,0741    -0,1081     0,0206    -2,4329

  16     129,6000   129,5907     0,0093     0,0135     0,0206     0,3041

  17     164,5000   164,5157    -0,0157    -0,0262     0,0232    -0,5516

  18     156,1000   156,1102    -0,0102    -0,0208     0,0262    -0,3953

  19     111,7000   111,7074    -0,0074    -0,0100     0,0187    -0,2340

  20     109,6000   109,5935     0,0065     0,0099     0,0215     0,2173

  21     146,7000   146,7324    -0,0324    -0,0593     0,0248    -1,1921

  22     125,6000   125,6407    -0,0407    -0,0595     0,0206    -1,3381

  23     128,3000   128,2852     0,0148     0,0186     0,0166     0,4514

  24     139,1000   139,0907     0,0093     0,0116     0,0166     0,2821

  25     119,9000   119,9435    -0,0435    -0,0723     0,0232    -1,5251

  26     148,0000   147,9963     0,0037     0,0050     0,0187     0,1170

  27     150,1000   150,0602     0,0398     0,0662     0,0232     1,3953

---------------------------------------------------------------------------

   R denote values with large absolute values of the standartised residual (>2)

---------------------------------------------------------------------------

 T(0,025,18)=2,10092; F(0,050,8,18)=2,51016

 Residual StDev=0,03678; R-sq=1,00000; Radj-sq=0,99999

 PRESS = 0,05967; R-sq(pred)=0,99999

 

This model is quite good. All correlation coefficients are equal to 1 with 18 degrees of freedom for the residual variance.  We can click “Copy to spreadsheet” to save the model in the spreadsheet:

 

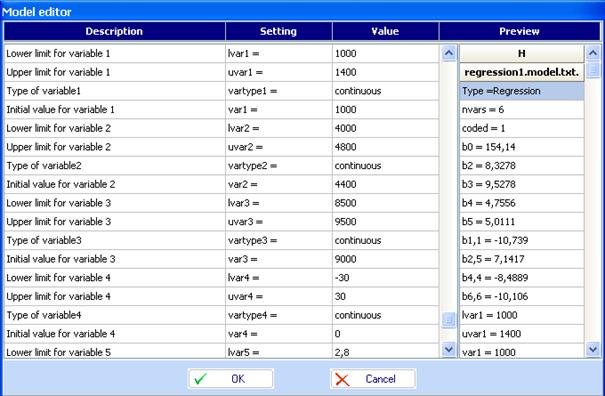
We will work in natural parameter values. That is why we introduce in the regression model all lower and upper levels of the factors. This can be done by use of Model editor. A fragment of these settings in the Model editor is given below:

 

 

The resulting regression model is:

 

 

Deriving mean and variance models with errors in factors

 

For the model-based approach we need the variance matrix of errors in factors

 

.

 

This is not given by Barker and Clausing. We computed estimates of these variances taking into account Taguchi's recommendation to choose the factor levels in the noise array equal to ,  and , where  is the mean value of i-th noise factor,  is the corresponding standard deviation, , and . Therefore, we can compute an estimate of the noise variance as follows:

 

.

 

The variances of the errors in coded factors can be obtained as follows:

 

.

 

They depend on and vary in the factor space.

 

This special situation can be taken into account with so called range factor for the standard deviation. Here it is

 

 

For most of the cases it is .

To create a model of the mean value in the case with errors in factors we use model editor. Click  to call it. Below is given an example for the model of mean values.

 

 

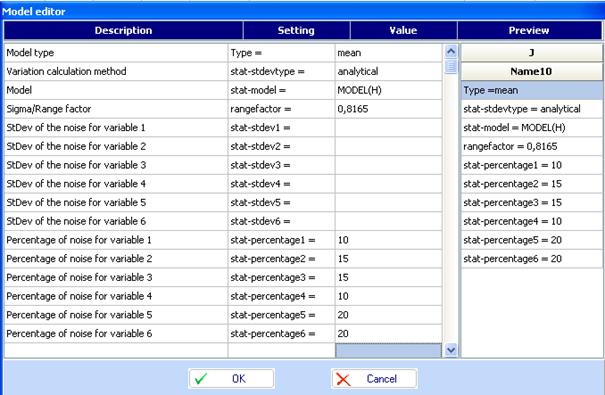
The model is shown in column I of file “Friction welding-Analytical-6.qsl”:

 

 

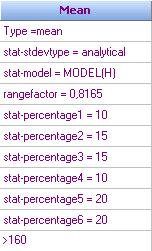
We called the model “Mean” and added an inequality >160, which instructs the program to search values of tensile strength > 160 during the optimization procedure.

 

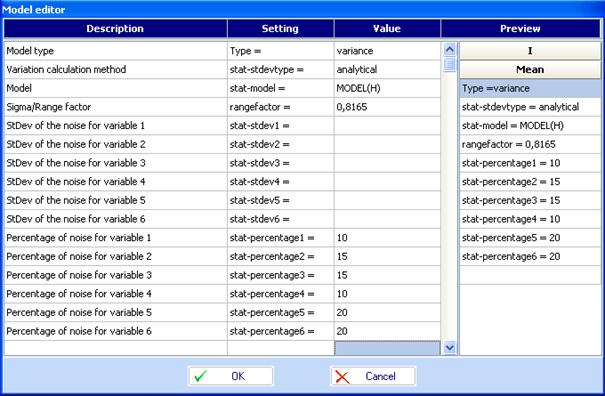
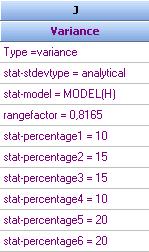
The model of variance is created also by use of model editor:

 

 

Click OK to get the following column in the spreadsheet for the variance function:

 

 

 

Optimization, contour plots, 3D plots.

 

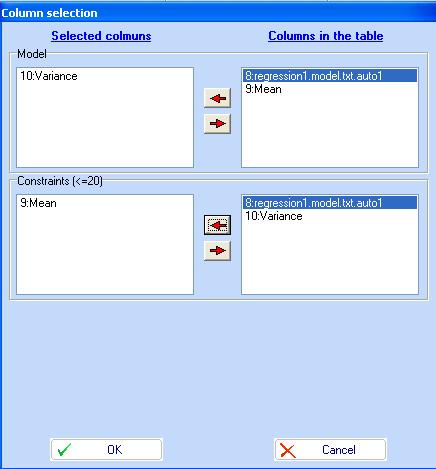
With the models defined above we can do optimization and draw contour plots. A good way to do that is to use the file: “Friction welding-Analytical-6.qsl” and to click the icon for contours .  We consider the Variance as a function to be minimized and the Mean as a constraint (Mean >160). This can be done by use of the Table for column selection:

 

 

Click OK to start contour drawing. The screen of the computer will look like that:

 

 

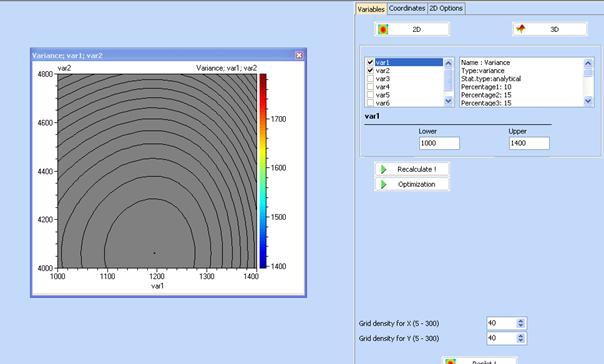
Click “Optimization” to start optimization procedure. Following will appear:

 

 

Click here to open sequences

 

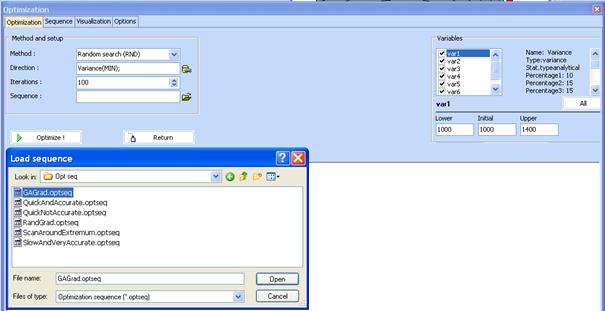
This window defines the starting method (Random search), direction (MIN), Iterations for the initial search (100) and selection of sequence of optimization methods which becomes active after the end of the random search (GAGrad.optseq). The independent variables should be chosen for the search and their initial values too. After selection of a sequence click “Optimize!” to start the procedure.

 

 

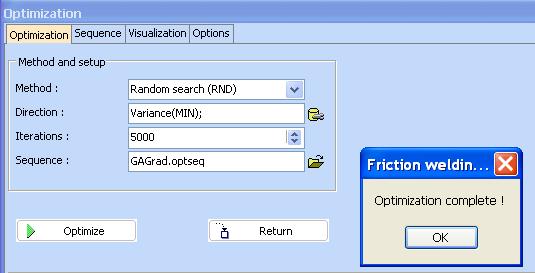
When optimization is completed click “Return”. Following will be seen:

 

 

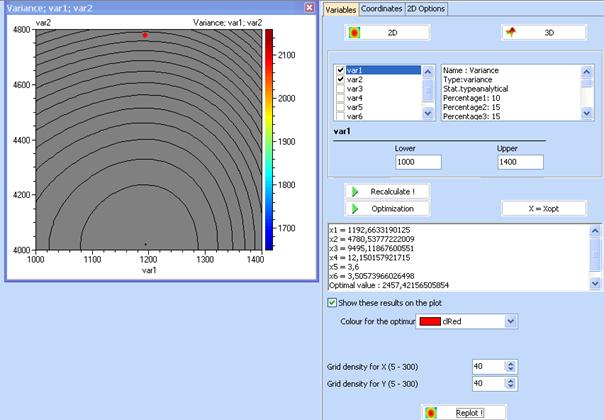
The optimal parameter values are given in the right hand side of the screen. Mark “Show these results on the plot” to get the optimal point. Note however that the plot shown on the figure above does not correspond to optimal factor values. To get a plot for the case when all factors are set on their optimal values click “X = Xopt”. Then following contour plot will be obtained:

 

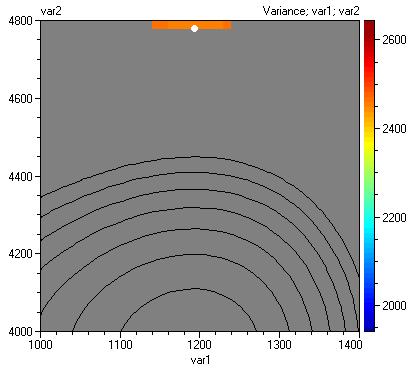
Some refinement of the border can be achieved by increasing grid density for both variables. The Figure above is obtained with grid density 40. If we change it to 100:

 

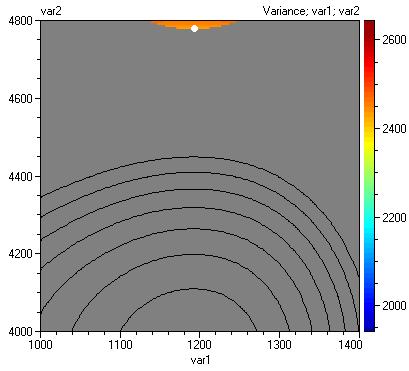
Following contours are obtained:

 

 

Three dimensional plots are also available. Click “3D” to draw a 3D plot. Then use “3D options” to refine the picture. A 3D plot for the same case is given below.

 

 

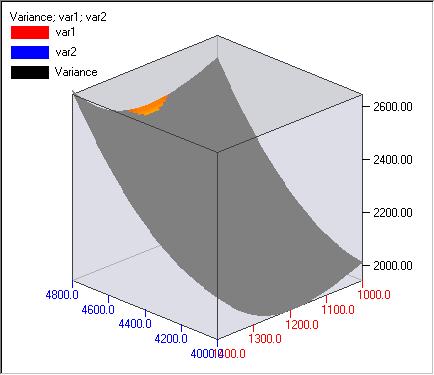
Tolerance design

 

A model based tolerance design can also be done. We use the same reduction of tolerances as Barker & Clausing to get comparable results. The tolerances are reduced as follows:

 

SPEED: 1200  10%    (no change)

HTPRS: 4800   5 %    (1/3 of the original)

UPPRS: 9500   7.5 % (1/2 of the original)

LENGTH:     0   10 %  (no change)

HTTIME:    3.6    5 %  (1/4 of the original)

UPTIME:    3.6    5 %  (1/4 of the original)

 

Using the model editor we define new models, denoted in file: “Friction welding-Analytical-6.qsl” as Mean-T and Variance-T. For example for Mean-T we define following parameters:

 

 

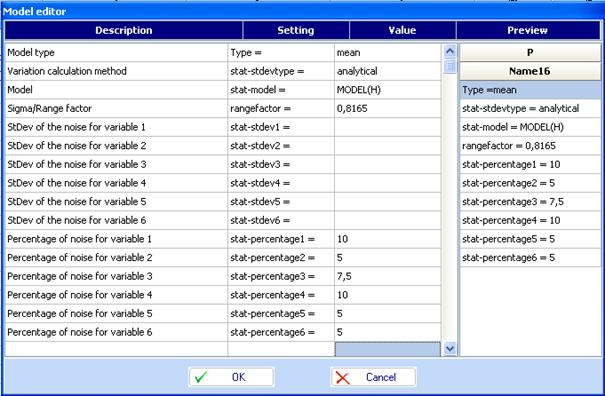
The mean and variance models are defined as follows:

 

 

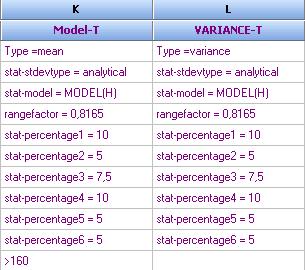
The optimal parameters are now:

 

 

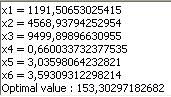
The standard deviation is , which is less than the obtained by Barker and Clausing (16.80). The mean strength is 160 as required.

 

The next figure shows contour plot of Variance-T and Mean-T after tolerance tightening.

 

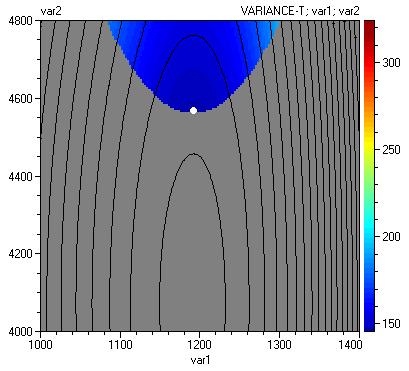
This plot can be additionally refined by putting border on the mean value contour equal to 160 and by changing thickness and colour of the line as follows:

 

 

As a result we obtain following plot:

 

 

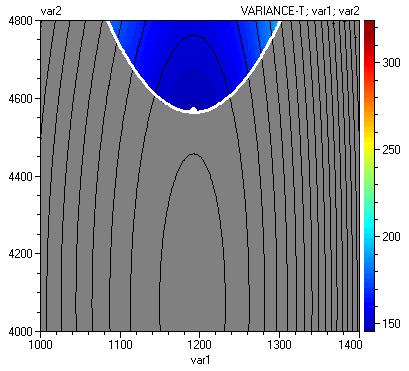
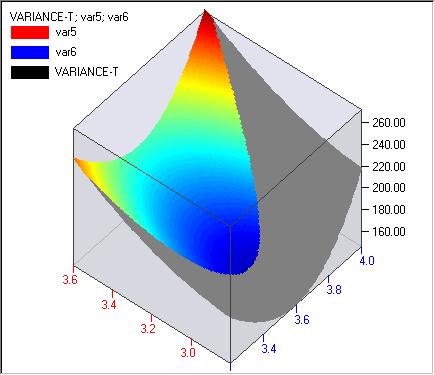
The next figure is a 3D plot:

 

 

 

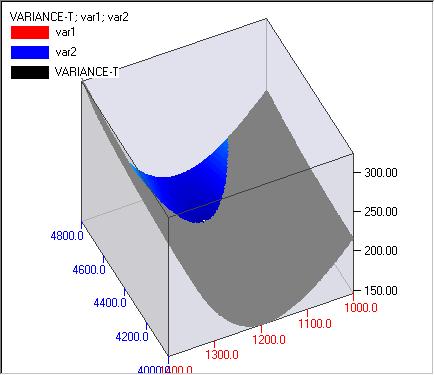
Other contour plots can also be obtained the same way. Contour and 3D plots for p5 and p6 are given below.

 

 

 

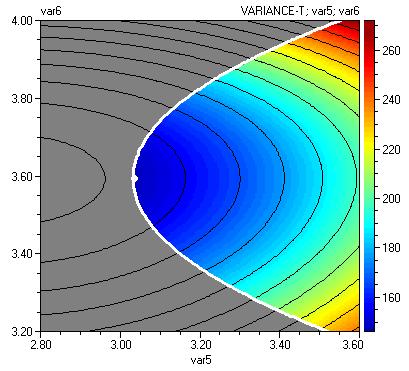
Conclusions

 

• Using model-based approach we obtained results, which are at least as good as the results obtained with Taguchi method. They are better with respect to the variance.
• The number of experiments with the model based approach is about 20 times less than for Taguchi method (Model based approach uses 27 runs, Taguchi method uses 522 runs).
• The model-based approach provides better optimization and graphical procedures.