Калкулатор на разпределения 

 

QSTATLAB дава възможност да се намират критичните точки на следните често използвани статистически разпределения: стандартно нормално разпределение, разпределение на Стюдънт (t – разпределение), - разпределение и разпределение на Фишер (F – разпределение).

 

Опцията Калкулатор на разпределения  може да бъде избрана от менюто "Диаграми и методи" или чрез иконката . Появява се показаното по-долу меню за избор на разпределение.

 

·         Стандартно нормално разпределение.  Тази програма изчислява интеграла 

 

            .

 

където  е нормално разпределена случайна величина със средно  и стандартно отклонение , а  е нормирана променлива

 

            .

 

 

 

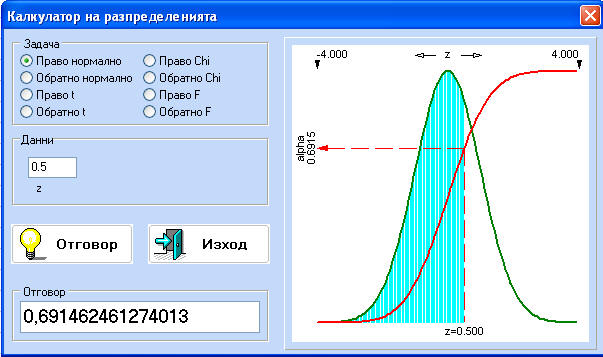
Има две възможности: Нормално и обратно нормално разпределение. Когато се избере Нормално в прозореца “Данни” трябва да се въведе . След това на вертикалната ос може да се отчете стойността на алфа , която е равна на стойността на . Тя показва вероятността за появяване на случайната величина  на ляво от някаква зададена стойност .

 

Като се използва стандартното нормално разпределение може да се намери вероятността за появяване на нормално разпределена случайна вличина в зададен интервал . Тя се изчислява така:

 

.

 

Пример. Ще намерим  вероятността за попадане на нормално разпределена случайна величина в интервала , при предположение, че средната й стойност е m = 3 и стандартноото отклонение е . Най-напред ще изчислим:

 

             и.

 

Кликнете “Право нормално”. Въведете в прозореца "Данни" на калкулатора  и кликнете "Отговор". В полето "Отговор" се появява  = 0.158655253931457. По подобен начин можем да намерим  = 0.308537538725987. След закръгляване изчисляваме вероятността за появяване на  в интервала  :

 

            .

 

Опцията “Обратно нормално” се използва, за да се определи каква стойност на  се получава при зададена стойност на . Например, ако е зададено  = 0.158655253931457, тази стойност се записва в прозорчето “Данни”. След това се натиска бутона “Решение”, при което в полето “Отговор” се получава .

 

 

Опция “Обратно t”. При тази опция се изисква да се зададат две величини: ниво на значимост (alpha) и брой на степените на свобода (ni). При натискане на бутона “Решение” в полето “Отговор” се получава критичната стойност на разпределението на Стюдънт, съответстваща на зададените параметри.

 

Пример. Задаваме alpha = 0.05 и ni = 7. При натискане на бутона “Решение” в полето “Отговор” се получава критичната стойност на разпределението на Стюдънт, която в случая е 1.89457860509001.

 

Опция “Право t”. В този случай при зададени критична стойност на разпределението на Стюдънт и брой на степените на свобода се получава съответното ниво на значимост.

 

Пример. Задаваме t = 1.833 и ni = 9. При натискане на бутона “Решение” в полето “Отговор” се получава alpha = 0.0500089700252915.

 

 

Опция “Обратно Chi”. При тази опция се изисква да се зададат две величини: ниво на значимост (alpha) и брой на степените на свобода (ni). При натискане на бутона “Решение” в полето “Отговор” се получава критичната стойност на - разпределението, съответстваща на зададените параметри.

 

Пример. Задаваме alpha = 0.05 и ni = 15. При натискане на бутон “Решение” в полето “Отговор” се получава критичната стойност на - разпределението 24.9957901397286.

 

Опция “Право Chi”. В този случай при зададени критична стойност на - разпределението и брой на степените на свобода се получава съответното ниво на значимост.

 

Пример. Задаваме  = 10.283 и ni = 21. При натискане на бутона “Решение” в полето “Отговор” се получава alpha = 0.974998498319471.  = 10.283 е стойността над която площта, определена от - разпределението  е равна на alpha.

 

 

Опция “Обратно F”. При тази опция се изисква да се зададат три величини: ниво на значимост (alpha), брой на степените на свобода за числителя (ni1) и брой на степените на свобода за знаменателя (ni2). При натискане на бутона “Решение” в полето “Отговор” се получава критичната стойност на F - разпределението, съответстваща на зададените параметри.

 

Пример. Задаваме alpha = 0.05, ni1 = 5, ni2 = 14. При натискане на бутон “Решение” в полето “Отговор” се получава критичната стойност на F - разпределението 2.9582489131222.

 

Опция “Право F”. В този случай при зададени критична стойност на F - разпределението и брой на степените на свобода се получава съответното ниво на значимост.

 

Пример. Задаваме F = 5.4967, ni1 = 4, ni2 = 17. При натискане на бутона “Решение” в полето “Отговор” се получава alpha = 0.00499995529867125.

 

 

Обратно към статистически методи