Обратно към Статистически анализ
Пропорции и доверителни интервали за пропорции
Много често класифицираме данните в една от две категории: годно/дефектно или минава/не минава или приема се/отхвърля се.
Пример 1. Да предположим, че на една производствена линия има 5 машини: A,B,C,D и E. В една извадка от n = 103 дефектни изделия n1 = 15 са произведени на машина А, n2 = 27 - на машина В, n3 = 31 - на машина С, n4 = 19 - на машина D и n5 = 11 - на машина Е.
Да означим пропорцията (относителната честота) на дефектните изделия, произведени от съответните машини като
Ако
можехме да направим безкраен брой наблюдения щяхме да получим вероятностите
за
поява на дефектни изделия на съответната машина. В
този раздел ще работим при следните допускания:
Разпределението на пропорциите не е нормално, а при приетите предположения е мултиномиално.
Доверителният интервал за която и да е пропорция е:
където 
е критичната стойност на стандартното нормално разпределение (с нулево средно и
дисперсия равна на 1) при ниво на значимост a. За a = 0.05 се
получава
.
Можем
да намерим доверителен интервал за разликата между две пропорции: 
, за да преценим има ли съществени разлики между истинските им стойности.
Неговите граници са:
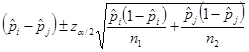
Проверка на хипотеза за равенство на пропорции.
Нулевата хипотеза
е: 
. За разглеждания пример
k
= 5 и предполагаемата пропорция е 0.2.
Нулевата хипотеза се приема, ако предполагаемата стойност попада в доверителните интервали за всички пропорции.
Нулевата
хипотеза: може да се провери и по следния
начин:
-
Изчислява
се:
-
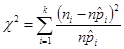
Нулевата
хипотеза се приема ако
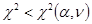, като
n
= k - 1
В програмата се появява вероятност Р, която трябва да е по-голяма от 0.05, за се приеме нулевата хипотеза. Ако Р < 0.05 нулевата хипотеза се отхвърля.
Алгоритъмът работи
добре, ако
Проверка на хипотеза за незначимост на разлика между две пропорции.
Нулевата хипотеза
е: 
.
Нулевата хипотеза се приема, ако доверителните интервали за разликите на всички двойки пропорции съдържат нулата.
Пример: Въвеждане на данните в QstatLab
В QstatLab данните за Пример 1 се подреждат в един ред (файл Contingency.qsl намиращ се в директория Primeri)
Кликва се върху иконката за базова статистика и се отваря следното меню:
Изберете “Дискретни величини:Пропорции и доверителни интервали”. Появява се меню за избор на колони.Прехвърлете имената на всички колони, съдържащи информацията от дясно в ляво (Бройки):
Появява се значителна по обем информация, която ще анализираме на 3 части:
А) Хи-квадрат тест за пропорции
Тъй като Р = 0,0095 < 0.05, хипотезата за равенство на всички пропорции се отхвърля. За това кои пропорции се различават най-много от предполагаемата стойност (1/к) = 0.02 се съди по това за кои машини компонентите на Хи-квадрат са най-голями. Най-голяма е компонентата 5,25049 за машина С. На тази машина се получават много повече дефекти (31) от очакваните (20,6). Следващата по големина компонента 4,47379 е за машина E. За нея наблюдаваният брой дефекти (11) е много по-малък от очаквания (20,06).
Б) Индивидуални доверителни интервали
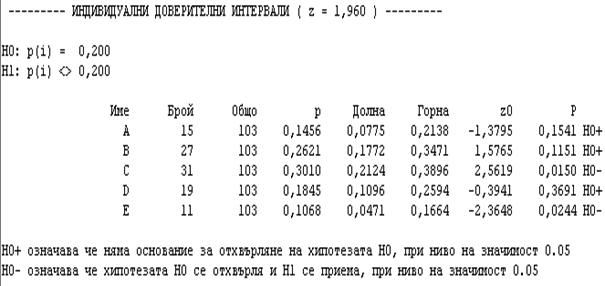
Означенията са следните:
· Брой е броят на дефектите, наблюдавани на съответната машина A,B,C,D или Е
· Общият брой дефекти е 103 = 15+27+31+19+11
·
р е пропорцията за съответната машина.
Например за машина А тя е равна на 0,1456 и е изчислена от отношението 15/103.
Във формулите по-горе е означена като 
· „Долна“ и „Горна“ са границите на доверителния интервал
Отхвърля се хипотезата, че всички пропорции са равни на 0.2, защото предполагаемата стойност 0.2 не попада в доверителните интервали за C и Е. Пропорцията на дефектните изделия е по-голяма от 0.2 за машина С и по-малка от 0.2 за машина Е.
В) Доверителни интервали за разлика между две пропорции
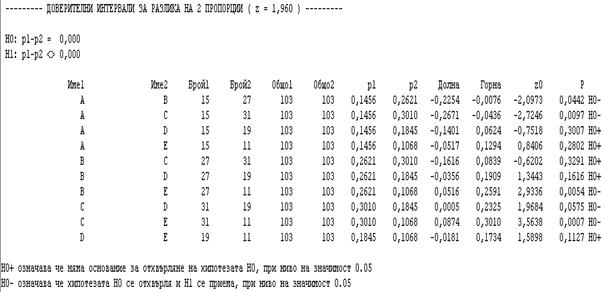
В тази задача „Горна“ и „Долна“ са границите на
доверителния интервал за разликата между пропорциите 
. Хипотезата за равенство на
двете пропорции се приема, ако в границите на доверителния интервал се намира
нулата.
За примера: отхвърля се хипотезата, че разликите между всички пропорции са незначими. Наблюдават се съществени разлики между следните двойки пропорции: А и B, A и C, B и E, C и D, C и E.
Хи-квадрат тест за двувходови таблици
В тази задача се изследва дали дадени категорийни данни зависят от два фактора. Може да се разглежда като двуфакторен дисперсионен анализ за категорийни данни.
Пример 1. Изследва се работата на 3 доставчика: A,B,C. Направени са 287 наблюдения за 1 година, като доставките без никакви пропуски са отбелязани с ОК, а тези с пропуски (закъснения, непълна комплектовка, сгрешена документация и др.) – с NOK. Получени са следните резултати Данните са дадени във файла Contingency.qsl):
При настройките на колоните първата колона (в примера „Качество“) се оформя като „Признак“, останалите като „Данни“.
Въпросът е: Има ли разлики в качеството на изпълнение на доставките за тримата доставчика?
На статистически език тази задача може да се разглежда като задача за проверка на хипотези Дефинират се следните хипотези:
Нулева хипотеза: Класификациите по редове и стълбове са независими
Алтернатива: Класификациите по редове и стълбове са зависими
Въвеждаме следните означения:
•
- брой на редовете в таблицата
•
- брой на колоните в таблицата
•
- сума на
i-тия ред
•
- сума на
j-тата колона
•
- число в клетката на
i-тия ред и
j-тата колона
Процедура:
1. Изчислява се:
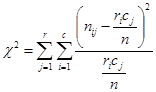
2.
Нулевата
хипотеза се приема ако , като
В програмата се появява вероятност Р, която трябва да е по-голяма от 0.05, за се приеме нулевата хипотеза. Ако Р < 0.05 нулевата хипотеза се отхвърля.
Алгоритъмът работи добре, ако
оцененият очакван брой събития 
във всяка клетка на таблицата е по-голям
от 5
Решение на примера с QstatLab:
Извикването на програмата става така:
След кликване на „Дискретни величини: Хи-квадрат тест“ се прави избор на колоните както следва:
Като се кликне „Приеми“ се получава следното решение:
Тъй като P < 0,05 се приема, че факторът „Доставчик“ влияе съществено върху резултатите. За разликите в резултатите се съди по компонентата на Хи-квадрат. Тя е най-голяма за фирма В. За нея разликите между очкваните и наблюдаваните стойности на доставките с качество ОК и NOK е най-голяма. Наблюдавани са 26, а са очаквани 36 доставки с качество ОК. Също наблюдаваните доставки с качество NOK са 21, докато очакваните са 11.
Броят на категориите за всеки фактор (нивата на факторите) може да бъде произволен. Илюстрация на това е следният пример.
Пример 2. Един от критериите за оценяване на работниците в един завод е броят на дефектните изделия на 1000 произведени. Работата е монотонна и се очаква, че след началния период на тренинг ще настъпи влошаване на мотивацията на хората. Изследват се 100 работника, разделени на 3 категории: А – до 1 година стаж, B – от 2 до 5 години стаж и C – от 6 до 10 години стаж. Дефектността за всеки от тях се оценява в три категории: висока, средна и ниска. Задачата е да се провери дали дефектността зависи от трудовия стаж (файл Contingency.qsl).
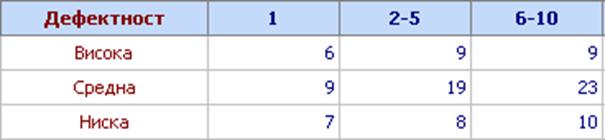
Извикването на програмата става както в Пример 1. В резултат на изчисленията се получава:
Тъй като P > 0,05 се приема, че факторът „Трудов стаж“ е незначим. Дефектността не зависи от трудовия стаж.