Заваряване чрез триене

 

Източници:

1. Barker, T, Clausing D. (1984). Quality engineering by design. The Taguchi method. The International QC forum. 11, No.8,28-52.
2. Vuchkov, I.N., Boyadjieva, L.N. (2001). Quality improvement with design of experiments. A response surface approach. Kluwer Academic Publishers, Dordrecht.

 

Методи:

Изчисления с електронна таблица, метод на Тагучи, Дисперсионен анализ, Регресионен анализ, Аналитични модели в робастното инженерство, Оптимизация, контурни диаграми, 3D диаграми

 

Файлове: Friction welding – Loss function 1.qsl, Friction welding – Param design 2.qsl, Friction welding – Verification 3.qsl, Friction welding – Loss function 1.qsl, Friction welding – Tolerance design 4.qsl, Friction welding – Regression 5.qsl, Friction welding – Analytical - 6.qsl.

 

Кратко описание на проблема:

 

Barker and Clausing (1984) използват метода на Тагучи за намиране на система за заваряване, която намалява или премахва счупването на вала на витлото на мощна извънбордна машина. Характеристика на качеството у е якостта на опън. Целта е да се получи у приблизително равна на 160 като се държи стандартното й отклонение под 20. Факторите са показани в табл.1. Ще означим с _,   стойностите на факторите в натуралните им физически мерни единици. Интервалите им на изменение са: .

 

Barker и Clausing използват кръстосан масив, състоящ се от ортогонален масив  в качеството на параметричен план (стълбове 2 до 7 в табл. 2) и ортогонален масив  като шумова матрица. Общият брой опити е . Вариациите на параметрите на процеса в толерансните граници, показани в табл.1 се разглеждат като шумове. Ортогоналният масив  се изпълнява за всеки ред на параметричния план. Нивата на шумовите фактори са избрани равни на  и  . Например за първия опит на табл. 2 първият параметър е  , което съответства на  rpm. Според табл. 2 нискостойностният толеранс на  е . Следователно нивата на  в масива  за първия ред на табл. 2 са 900, 1000 и 1100 rpm.

 

Таблица 1. Нива на факторите, нискостойностни толеранси и

полуинтервали на изменение  на факторите за примера на заваряване чрез триене.

 

Barker и Clausing не дават пълния кръстосан план. Те дават само параметричният план и якостта при опън у, стандартното отклонение на у и отношението сигнал-шум. Те са показани в табл. 2. Данните от табл. 2 са дадени също във файла Friction welding – Param design.qsl.

 

Таблица 2. Параметричен план, якост при опън,

стандартно отклонение и отношение сигнал/шум

 

Фрагмент на таблицата на QSTATLAB за този пример е даден по-долу

 

 

1.  Анализ на данни с метода на Тагучи (Barker & Clausing)

 

Функция на загубите:

Barker & Clausing изчисляват функцията на загубите на Тагучи:

 

,

 

където  е целевата стойност за якостта. Те оценяват, че намаляване на якостта на опън с 60 предизвиква загуби от $ 500. Замествайки тези стойности в L те получават:

 

 

Следователно

 

 

Ще изчислим функцията на загубите за стойности на якостта от 100 до 160, стъпка 10. QstatLab има вградена функция на загубите на Тагучи. Функция, наречена LOSS1(k; target; ymean; sigma) изчислява следната функция на загубите:

 

 

Можем да я използваме, за да изчислим  замествайки k = 0.1388889, target = 160, ymean =A1 and sigma = 0.

 

Кликнете  и изберете LOSS1(k; target; ymean; sigma) а след това въведете дадените по-горе стойности в скобите. Стойността в клетка B1 е 500.0004. Мъкнете надолу точката в дясния долен ъгъл на клетка B1 за да получите другите стойности на функцията на загубите. Резултатите са показани в колона В на таблицата по-долу.

 

 

Можем да начертаем функцията на загубите като използваме „Интерполации” на QstatLab (). Изберете колоните както е показано по-долу:

 

 

Кликнете OK за да получите следната диаграма:

 

 

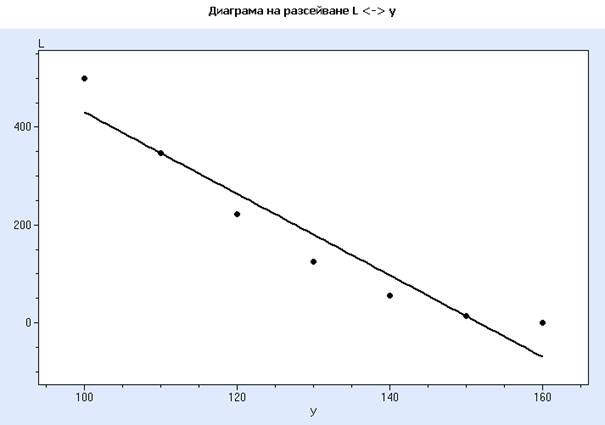
QSTATLAB използва по подразбиране линейна регресия за апроксимация на данните. Ясно е, че линейната апроксимация не апроксимира данните достатъчно добре. Ето защо кликнете „Настройки→Диаграма→Интерполация(L) → Вид линейна – y = a+bx” за да отворите следния прозорец:

 

 

Изберете полиномиална – y =b0+b1*x+…+bN*x^(N-1) и след това изберете  “Степен на полинома(L) = 2”:

Ще се получи следната графика:

 

 

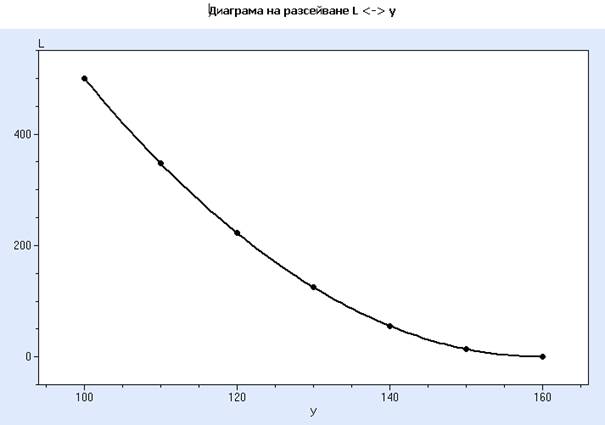
Както се очакваше статистическият анализ показва много добра апроксимация:

 

Основна информация за комплекта от данни y-L

------------------------------------------------------------------

Означено като X е y

Означено като Y е L

Брой елементи: 7

Средно за X = 130.0000

Средно за Y = 180.5556

Qx = 2800.0000

Qy = 210648.1819

Qxy = -23333.3352

Качество на интерполацията = 1.0000

Регресионно уравнение:     3556  -44.44*x+  0.1389*x^ 2

 

Статистически анализ и избор на стойности на параметрите чрез използване на дисперсионен анализ (ANOVA):

 

Методът на Тагучи използва дисперсионният анализ за да направи изводи за средното и отношението сигнал/шум. Да разгледаме най-напред приложението му за якостта при на опън (файл: Friction welding – Param design 2.qsl). Кликнете иконката  и изберете факторите и якостта на опън както е показано по-долу:

 

Кликнете ‘Приеми” за да получите следната таблица на дисперсионния анализ:

 

            Дисперсионен анализ (ANOVA) за y = STRENGTH - (p1 = SPEED;

            p2 = HTPRS; p3 = UPPRS; p4 = LENGTH; p5 = HTTIME; p6 = UPTIME)

-------------------------------------------------------------------------

   Означение                      Име   Бр. нива     Нива

          x1               p1 = SPEED          3     -1; 0; 1

          x2               p2 = HTPRS          3     -1; 0; 1

          x3               p3 = UPPRS          3     -1; 0; 1

          x4              p4 = LENGTH          3     -1; 0; 1

          x5              p5 = HTTIME          3     -1; 0; 1

          x6              p6 = UPTIME          3     -1; 0; 1

-------------------------------------------------------------------------

    Източник        Суми  Ст. свобода   Дисперсия           F           P

          x1   691.94296            2   345.97148     7.91359     0.00502

          x2  1248.33407            2   624.16704    14.27691     0.00042

          x3  1634.01407            2   817.00704    18.68785     0.00011

          x4   839.44296            2   419.72148     9.60052     0.00237

          x5   452.00519            2   226.00259     5.16948     0.02083

          x6   612.73407            2   306.36704     7.00770     0.00778

     Остатък   612.06074           14    43.71862

-------------------------------------------------------------------------

        Общо  6090.53407           26

 

Остатъчно СКО = 6.61201      R-sq = 0.89951      R-sq (adj) = 0.81337

 

Доверителни интервали за средната стойност по всяко факторно ниво:

Доверителните интервали са построени на база на стандартното отклонение

за всяко ниво на факторите.

 

      Ниво   Брой  Средно    Дисперсия       95% Доверителен интервал

p1 = SPEED

        -1     9 131.01111   228.14861     119.4007 <= 131.0111 <= 142.6215

         0     9 141.74444   202.17278     130.8149 <= 141.7444 <= 152.6739

         1     9 131.00000   244.50250     118.9807 <= 131.0000 <= 143.0193

p2 = HTPRS

        -1     9 126.25556   203.83278     115.2813 <= 126.2556 <= 137.2298

         0     9 134.58889   118.24111     126.2305 <= 134.5889 <= 142.9473

         1     9 142.91111   283.20111     129.9755 <= 142.9111 <= 155.8467

p3 = UPPRS

        -1     9 125.05556   174.37028     114.9053 <= 125.0556 <= 135.2058

         0     9 134.58889   264.62611     122.0847 <= 134.5889 <= 147.0931

         1     9 144.11111   118.06861     135.7588 <= 144.1111 <= 152.4634

p4 = LENGTH

        -1     9 127.00000   219.31500     115.6166 <= 127.0000 <= 138.3834

         0     9 140.24444   246.66028     128.1722 <= 140.2444 <= 152.3167

         1     9 136.51111   190.41111     125.9043 <= 136.5111 <= 147.1179

p5 = HTTIME

        -1     9 129.56667   246.34750     117.5021 <= 129.5667 <= 141.6313

         0     9 134.60000   148.51500     125.2325 <= 134.6000 <= 143.9675

         1     9 139.58889   309.95361     126.0561 <= 139.5889 <= 153.1217

p6 = UPTIME

        -1     9 131.22222   366.31444     116.5104 <= 131.2222 <= 145.9340

         0     9 141.32222    94.82944     133.8369 <= 141.3222 <= 148.8075

         1     9 131.21111   223.58111     119.7175 <= 131.2111 <= 142.7047

 

 

По-долу са дадени графики на главните ефекти за якостта. Резултатите от този анализ показват, че всички фактори са значими при ниво на значимост 0.05.

 

 

 

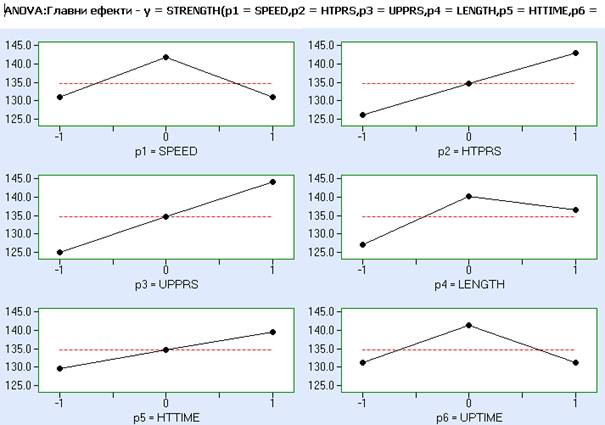
Ще разгледаме резултатите от дисперсионния анализ за отношението S/N:

 

            Дисперсионен анализ (ANOVA) за S/N - (p1 = SPEED; p2 = HTPRS;

            p3 = UPPRS; p4 = LENGTH; p5 = HTTIME; p6 = UPTIME)

-------------------------------------------------------------------------

   Означение                      Име   Бр. нива     Нива

          x1               p1 = SPEED          3     -1; 0; 1

          x2               p2 = HTPRS          3     -1; 0; 1

          x3               p3 = UPPRS          3     -1; 0; 1

          x4              p4 = LENGTH          3     -1; 0; 1

          x5              p5 = HTTIME          3     -1; 0; 1

          x6              p6 = UPTIME          3     -1; 0; 1

-------------------------------------------------------------------------

    Източник        Суми  Ст. свобода   Дисперсия           F           P

          x1   132.32519            2    66.16259     2.68054     0.10337

          x2   165.83407            2    82.91704     3.35933     0.06432

          x3    79.33407            2    39.66704     1.60709     0.23534

          x4    74.03630            2    37.01815     1.49977     0.25694

          x5    24.89407            2    12.44704     0.50428     0.61450

          x6   736.44519            2   368.22259    14.91831     0.00034

     Остатък   345.55630           14    24.68259

-------------------------------------------------------------------------

        Общо  1558.42519           26

 

Остатъчно СКО = 4.96816      R-sq = 0.77827      R-sq (adj) = 0.58821

 

Доверителни интервали за средната стойност по всяко факторно ниво:

Доверителните интервали са построени на база на стандартното отклонение

за всяко ниво на факторите.

      Ниво   Брой    Средно   Дисперсия       95% Доверителен интервал

p1 = SPEED

        -1      9  33.15556    90.41778     25.8464 <= 33.1556 <= 40.4647

         0      9  38.24444    11.41028     35.6480 <= 38.2444 <= 40.8409

         1      9  34.07778    76.43444     27.3576 <= 34.0778 <= 40.7980

p2 = HTPRS

        -1      9  31.65556   129.06278     22.9230 <= 31.6556 <= 40.3881

         0      9  36.83333    20.67500     33.3382 <= 36.8333 <= 40.3284

         1      9  36.98889    24.33611     33.1969 <= 36.9889 <= 40.7809

p3 = UPPRS

        -1      9  32.75556    79.82278     25.8880 <= 32.7556 <= 39.6231

         0      9  36.63333    20.79000     33.1285 <= 36.6333 <= 40.1382

         1      9  36.08889    84.27361     29.0325 <= 36.0889 <= 43.1453

p4 = LENGTH

        -1      9  35.20000    19.62750     31.7946 <= 35.2000 <= 38.6054

         0      9  37.16667    24.34250     33.3742 <= 37.1667 <= 40.9591

         1      9  33.11111   141.57861     23.9650 <= 33.1111 <= 42.2572

p5 = HTTIME

        -1      9  36.48889    16.74361     33.3436 <= 36.4889 <= 39.6342

         0      9  34.25556    93.96528     26.8044 <= 34.2556 <= 41.7067

         1      9  34.73333    80.98250     27.8161 <= 34.7333 <= 41.6506

p6 = UPTIME

        -1      9  37.25556    10.23028     34.7970 <= 37.2556 <= 39.7141

         0      9  40.24444     0.91278     39.5101 <= 40.2444 <= 40.9788

         1      9  27.97778    91.60444     20.6208 <= 27.9778 <= 35.3347

 

 

Таблицата на дисперсионния анализ показва, че значими ефекти за отношението S/N са UPTIME при ниво на значимост 0.05, SPEED и HTPRS при ниво на значимост 0.1.  Съответните главни ефекти са показани по-долу:

 

 

 

Barker & Clausing правят следните заключения на базата на графиките за главните ефекти за якостта и отношението S/N:

 

„Нашият анализ показа, че три от факторите имат значим ефект върху S/N (‘контролни фактори’), докато другите три влияят значимо само на нивата на средното (‘сигнални фактори”). Това е предимство, тъй като можем да използваме контролните фактори, зада поддържаме вариацията на подходящи нива и да изменяме средното с помощта на сигналните фактори. Нашите графики показват как да настроим параметрите. Скоростта е най-добра при средното й ниво 1200 RPM. Най-доброто налягането при загряване е 4800 psi. Налягането при притискане е сигнален фактор и се установява на 9500 psi да максимизира средната якост. Най-добрата дължина е при нула отклонение от номинала. Времето за загряване дава най-добър сигнал при 3.6 sec, макар, че S/N е най-добро при 2.8. Понеже този фактор не показва статистически значим ефект за S/N ние задаваме това ниво в полза на средната стойност на отклика. Времето при притискане е най-добро при 3.6 или средното ниво.”

 

Толерансно планиране:

 

Barker & Clausing са изпълнили толерансен план L18 за да се потвърдят резултатите, получени чрез анализа на параметричния план. В този план те използват оптималните стойности, намерени чрез параметричния план и въвеждат шумове в съответствие с нискостойностните толеранси, дадени в табл.1 (Friction welding – Verification 2.qsl):

 

SPEED: 1200  10%

HTPRS: 4800  15%

UPPRS: 9500  15%

LENGTH:     0  10%

HTTIME:   3.6  20%

UPTIME:   3.6  20%

 

Данните са показани в следващата таблица:

 

 

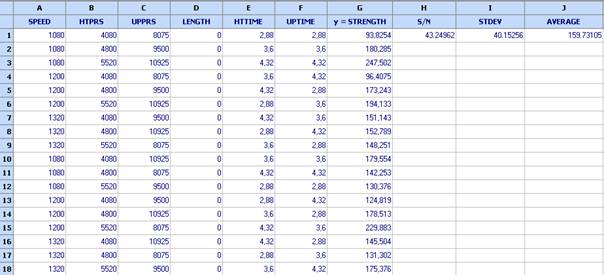
Изчисляването на отношението сигнал/шум може да стане чрез вградената формула STN3(G1:G18). Тя е:

 

 

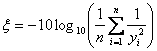
Отношението S/N е 43.25. Изчисляваме и стандартното отклонение по формулата =STDEV(G1:G18). Резултатът е STDEV = 40.15256. Vuchkov & Boyadjieva (2001) показват, че тази стойност е изместена и че истинската стойност е около 50.  

 

Средното на якостта при опън в потвърдителния експеримент се изчислява по формулата: =AVERAGE(G1:G18). Резултатът е: 159,73105. Средната якост е близка до желаната, но стандартното отклонение е все още твърде голямо. Загубите са също голями: : . За да намалят загубите Barker & Clausing стесняват толерансите. Най-напред те изчисляват приносите на факторите на базата на таблицата за дисперсионния анализ за масива L18: (файл: Friction welding – Verification 3.qsl):

 

 

 

 

 

 

            Дисперсионен анализ (ANOVA) за y = STRENGTH - (SPEED; HTPRS;

                            UPPRS; LENGTH; HTTIME; UPTIME)

-------------------------------------------------------------------------

   Означение                      Име   Бр. нива     Нива

          x1                    SPEED          3     1080; 1200; 1320

          x2                    HTPRS          3     4080; 4800; 5520

          x3                    UPPRS          3     10925; 8075; 9500

          x4                   LENGTH          1     0

          x5                   HTTIME          3     2,88; 3,6; 4,32

          x6                   UPTIME          3     2,88; 3,6; 4,32

-------------------------------------------------------------------------

    Източник        Суми  Ст. свобода   Дисперсия           F           P

          x1   774.44053            2   387.22027     1.01216     0.41105

          x2  9311.26356            2  4655.63178    12.16938     0.00527

          x3  5598.36737            2  2799.18368     7.31680     0.01927

          x4     0.00000            0     0.00000     0.00000

          x5  5732.72390            2  2866.36195     7.49240     0.01821

          x6  3313.09952            2  1656.54976     4.33006     0.05971

     Остатък  2677.98530            7   382.56933

-------------------------------------------------------------------------

        Общо 27407.88018           17

 

Остатъчно СКО = 19.55938      R-sq = 0.90229      R-sq (adj) = 0.76271

 

Приблизително изчисление на приносите се базира на сумите на квадратите в таблицата на дисперсионния анализ и е дадено по-долу.

 

 

Например приносът на налягането при нагряване към изменчивостта е:

 

 

Използвайки тази информация е решено да се намалят толерансите на факторите както следва:

 

SPEED: 1200  10%    (без изменение)

HTPRS: 4800   5 %    (1/3 от оригинала)

UPPRS: 9500   7.5 % (1/2 от оригинала)

LENGTH:     0   10 %  (без изменение)

HTTIME:    3.6    5 %  (1/4 от оригинала)

UPTIME:    3.6    5 %  (1/4 от оригинала)

Barker & Clausing изпълняват нов L18 за да проверят ситуацията след свиването на толерансите. Планът е показан в таблицата по-долу (файл: Friction welding – Tolerance design – 4)

 

 

 

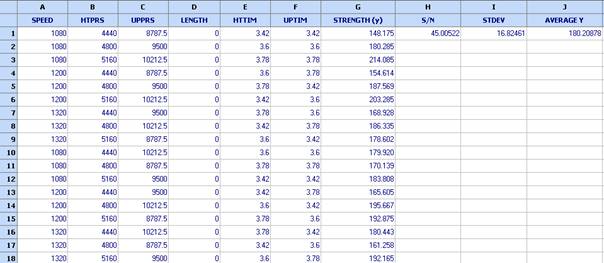
Изчислението на отношението сигнал/шум (S/N), стандартното отклонение и средното на у е направено с вградените функции както беше показано по-горе.

 

Може да се види, че след толерансното планиране стандартното отклонение е намалено до 16.82 (преди толерансното планиране е било 40.15). Средната якост е увеличена до 180.21 (била е 159.53).

 

Barker & Clausing съобщават за намаляване на загубите от $ 350/машина до $22/машина. За 10000 машини това прави икономия над $ 3 милиона.

 

Изводи:

 

• Изпълненият от Barker & Clausing експеримент е дало възможност за увеличаване на якостта на опън до 180 и намаляване на стандартното отклонение до 16.82.
• В резултат на това са намалени загубите, което води до икономии над $3 милиона.
• За получаване на тези резултати Barker & Clausing са изпълнили параметричен план с 27x18 = 486 опита и потвърдителен експеримент с 18 опита и толерансен план с 18 опита. Общият брой опити е 522.
• Оптималните стойности на параметрите са намерени приблизително, защото в метода на Тагучи са избрани само между нивата на параметрите в експеримента.

 

2.  Моделно-ориентиран подход към данните за заваряване чрез триене

 

Възможен е моделно ориентиран подход към същия проблем (Vuchkov, Boyadjieva (2001). Той намалява драстично броя на експериментите и осигурява по-сигурни изводи от метода на Тагучи.

Моделно ориентираният подход включва следните стъпки:

 

• Създаване на регресионен модел
• Извеждане на аналитични модели за средната стойност и дисперсията на характериостиката на качеството.
• Минимизиране на дисперсията при поддържане на средната стойност равна на целта уили минимизиране на функцията на загубите.

 

В случая с примера за заваряване чрез триене ще използваме само 27 от 522 опита за да получим  решението. Намаляването на броя на опитите е почти 20 пъти!

 

Създаване на регресионен модел

 

Най-напред ще препишем параметричния план в кодиран вид (файл: Friction welding – Regression – 5.qsl). Като се използва командата =CODE(A1;1000;1400) и като се мъкне надолу, получаваме първата колона на кодирания план. Другите колони на матрицата на параметричния план се кодират по подобен начин. По-долу е показан фрагмент от тази матрица с данните за якостта на опън (у). Всички данни са във файла Friction welding-Regression-5.qsl. Той съдържа също моделът, получен след изчисленията.

 

 

Искаме да създадем регресионен модел от втори ред за якостта на опън. Ще използваме регресионен анализ (). Стартираме с избор на колони както следва:

 

 

В този пример броят на неизвестните коефициенти в полином от втори ред с 6 фактора е 28, докато броят на опитите в параметричния план е само 27. Това означава, че информационната матрица е лошо обусловена (има мултиколинеарност). Всяка програма за регресионен анализ работи нестабилно при такива условия. QstatLab може да отстрани някои членове в регресията, за да избегне мултиколинеарността. Най-напред проверяваме дали има коефициенти с нулева стойност. За да използваме тази възможност настройваме свойствата на регресионния анализ както следва:

 

 

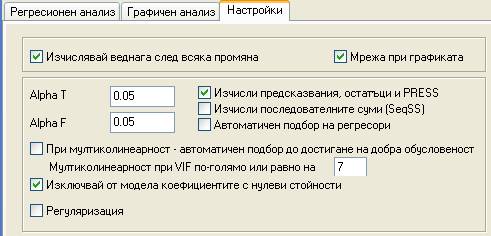
Кликнете  и изберете модел от втори ред:

 

Получаваме следното:

 

*** Броят на коефициентите ( 28) не бива да надвишава броя на избраните наблюдения ( 27)

Резултати :

***   Матрицата е лошо обусловена (норма: 5200503981.56435) => Получените резултати може да не са точни.

*** Коефициента b4,6  има нулева стойност и е изключен от модела

*** Коефициента b3,6  има нулева стойност и е изключен от модела

*** Коефициента b3,5  има нулева стойност и е изключен от модела

*** Коефициента b1,5  има нулева стойност и е изключен от модела

*** Коефициента b1,2  има нулева стойност и е изключен от модела

*** Коефициента b2,6  има нулева стойност и е изключен от модела

--------------------------------------------------------------------Наблюдения: 27

Входни променливи: 6

Брой избрани коефициенти: 22

Обозначения:

     x1 <--> p1

     x2 <--> p2

     x3 <--> p3

     x4 <--> p4

     x5 <--> p5

     x6 <--> p6

     y <--> y

--------------------------------------------------------------------

 

Много от регресионните коефициенти са близки до нулата. За да се изберат сами значимите коефициенти кликваме  и избираме полунормална графика на ефектите както следва:

 

Получената полунормална графика на ефектите е:

 

 

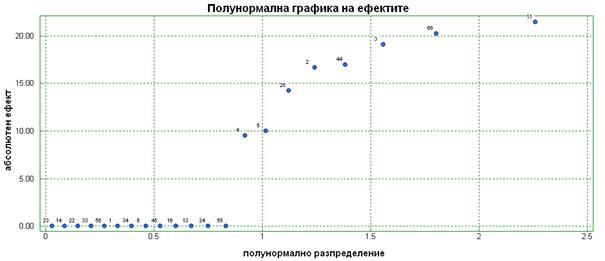
Можем да премахнем от модела всички коефициенти, които са близки до нула. Получаваме следното:

 

y = 154.141+8.328x2+9.528x3+4.756x4+5.011x5-10.739x1x1-8.489x4x4-10.106x6x6+7.142x2x5

---------------------------------------------------------------------------

   Регресор       Коеф    Ст.Откл          t          p   Значимост    VIF

         0     154.141      0.019   8230.393      0.000       +

         2       8.328      0.009    960.585      0.000       +      1.000

         3       9.528      0.009   1099.001      0.000       +      1.000

         4       4.756      0.009    548.539      0.000       +      1.000

         5       5.011      0.009    578.017      0.000       +      1.000

        11     -10.739      0.015   -715.163      0.000       +      1.000

        44      -8.489      0.015   -565.323      0.000       +      1.000

        66     -10.106      0.015   -672.986      0.000       +      1.000

        25       7.142      0.011    672.606      0.000       +      1.000

    Значимостта на коефициентите е определена при ниво = 0.05

---------------------------------------------------------------------------

                        Дисперсионен анализ (ANOVA)                       -

---------------------------------------------------------------------------

      Източник  Сума квадр.  Ст.Своб.  Дисперсия        F            P

      Модел     6090.50972      8      761.31372   562735.30886   0.00000

    Остатък        0.02435     18        0.00135

       Общо     6090.53407     26

---------------------------------------------------------------------------

               Предсказани стойности и остатъци                     

---------------------------------------------------------------------------

   N          y          yp        y-yp    PRESS(i)    SE pred. Ст. остатък

   1     104.3000   104.3269    -0.0269    -0.0446     0.0232    -0.9410

   2     135.1000   135.0741     0.0259     0.0350     0.0187     0.8190

   3     128.6000   128.6324    -0.0324    -0.0538     0.0232    -1.1357

   4     123.8000   123.7685     0.0315     0.0395     0.0166     0.9592

   5     134.6000   134.5741     0.0259     0.0326     0.0166     0.7899

   6     134.7000   134.6741     0.0259     0.0378     0.0206     0.8515

   7     150.6000   150.6213    -0.0213    -0.0390     0.0248    -0.7834

   8     116.2000   116.2269    -0.0269    -0.0408     0.0215    -0.9004

   9     151.2000   151.1519     0.0481     0.0650     0.0187     1.5210

  10     134.2000   134.1546     0.0454     0.0925     0.0262     1.7608

  11     134.1000   134.1046    -0.0046    -0.0077     0.0232    -0.1622

  12     132.0000   131.9907     0.0093     0.0135     0.0206     0.3041

  13     125.8000   125.7630     0.0370     0.0541     0.0206     1.2165

  14     140.9000   140.8963     0.0037     0.0050     0.0187     0.1170

  15   R 158.5000   158.5741    -0.0741    -0.1081     0.0206    -2.4329

  16     129.6000   129.5907     0.0093     0.0135     0.0206     0.3041

  17     164.5000   164.5157    -0.0157    -0.0262     0.0232    -0.5516

  18     156.1000   156.1102    -0.0102    -0.0208     0.0262    -0.3953

  19     111.7000   111.7074    -0.0074    -0.0100     0.0187    -0.2340

  20     109.6000   109.5935     0.0065     0.0099     0.0215     0.2173

  21     146.7000   146.7324    -0.0324    -0.0593     0.0248    -1.1921

  22     125.6000   125.6407    -0.0407    -0.0595     0.0206    -1.3381

  23     128.3000   128.2852     0.0148     0.0186     0.0166     0.4514

  24     139.1000   139.0907     0.0093     0.0116     0.0166     0.2821

  25     119.9000   119.9435    -0.0435    -0.0723     0.0232    -1.5251

  26     148.0000   147.9963     0.0037     0.0050     0.0187     0.1170

  27     150.1000   150.0602     0.0398     0.0662     0.0232     1.3953

---------------------------------------------------------------------------

   С R са обозначени наблюдения с голяма абсолютна стойност на стандартизирания остатък (>2)

---------------------------------------------------------------------------

 T(0.025,18)=2.10092; F(0.050,8,18)=2.51016

 Остатъчно СКО=0.03678; R-sq=1.00000; Radj-sq=0.99999

 PRESS = 0.05967; R-sq(pred)=0.99999

 

Този модел е много добър. Всички корелационни коефициенти са почти равни на 1 с 18 степени на свобода за остатъчната дисперсия. Можем да кликнем  за да запазим модела в таблицата:

 

 

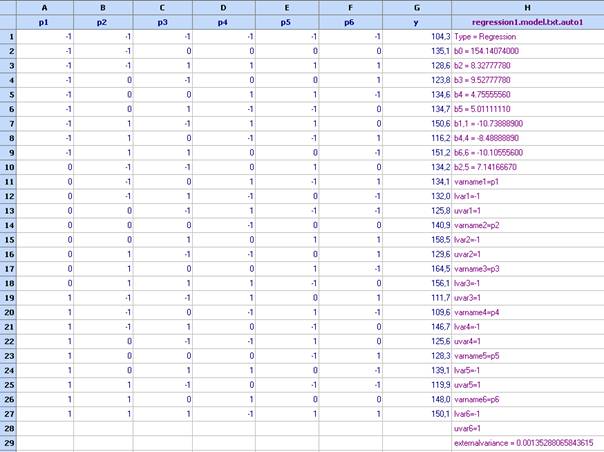
Ще работим с натурални стойности на параметрите. По тази причина въвеждаме в модела всички долни и горни нива на факторите. Това може да бъде направено чрез използване на редактора за въвеждане на модели (). Фрагмент от настройките на редактора за модели е даден по-долу:

 

 

Полученият регресионен модел е:

 

Извеждане на модели на средното и дисперсията при грешки във факторите

 

За моделно-ориентираният подход ние се нуждаем от матрицата на дисперсиите на грешките във факторите:

 

 

Тя не е дадена от Barker и Clausing. Изчисляваме грешките в тези оценки като вземаме предвид препоръките на Тагучи за избор на нивата на факторите в шумовата матрица както следва: ,  и , където  е средната стойност на i-тия шумов фактор,  е съответното стандартно отклонение, , и . Следователно можем да изчислим една оценка на средноквадратичното отклонение на шумовия фактор по следния начин:

 

 

Дисперсиите на грешките във факторите могат да бъдат получени както следва:

 

 

Те зависят от и се изменят в пространството на факторите.

 

Тази специална ситуация може да бъде взета предвид с т.н. Фактор Сигма/Обхват за стандартното отклонение. В случая той е:

 

 

В повечето случаи той е:

 

 

За да се съдаде модел за средната стойност в случая с грешки във факторите използваме редактора на модлеи. Кликваме  за да го извикаме. По-долу е даден пример за модела на средните стойности:

 

 

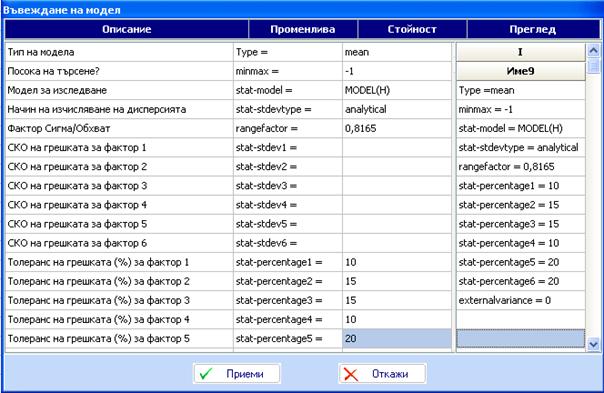
Моделът е показан в колона I на файла “Friction welding-Analytical-6.qsl”:

 

 

Означаваме модела като “Mean” и добавяме неравенството >160, което инструктира програмата да търси стойности на якостта на опън >160 при оптимизацията.

 

Моделът на дисперсията се създава по същия начин чрез моделния редактор:

 

 

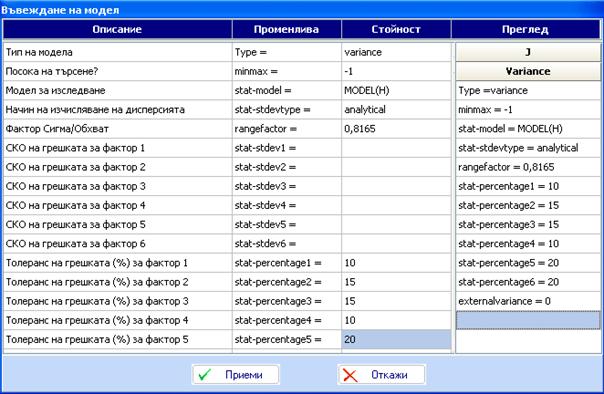
Кликваме «Приеми» за да получим следната колона в таблицата за дисперсията:

 

 

Оптимизация, контурни диаграми, 3D диаграми

 

С дефинираните по-горе модели можем да извършим оптимизация и да начертаем контурни диаграми. Добър начин да се извърши това е да се използва файла “Friction welding-Analytical-6.qsl” и да се кликне иконката за контурни диаграми:  . Функцията, която ще минимизирме е Variance, а средното е ограничение (Mean >160).. Това може да се направи като се използва таблицата за избор на колони:

 

 

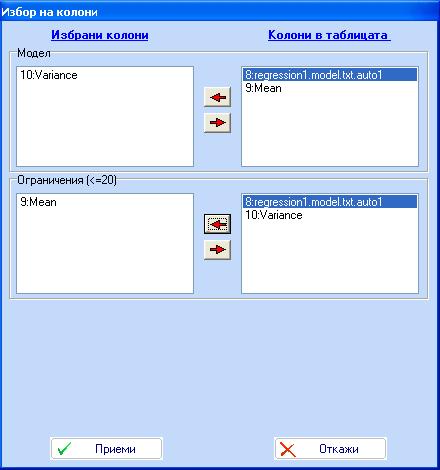
Кликнете «Приеми» за да започне чертаенето на контурите. Екранът на компютъра ще изглежда както следва:

 

 

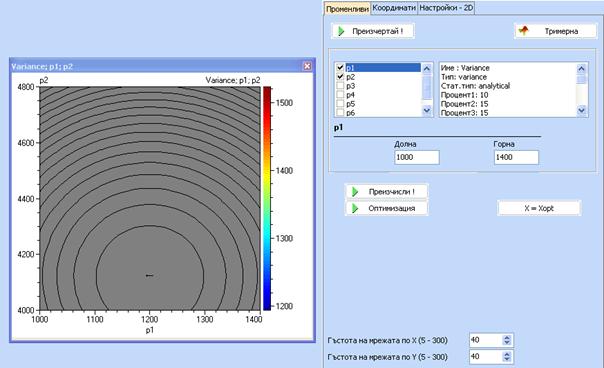
Кликнете 'Оптимизация' за да започнете оптимизационната процедура. Ще се появи следното:

 

 

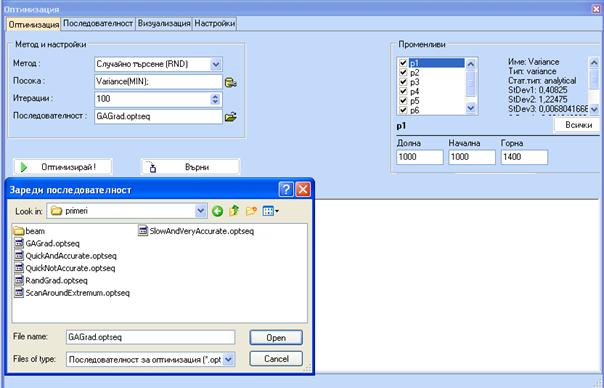
Този прозорец дефинира началният метод (Случайно търсене), направлението (MIN), итерациите за началното търсене (100) и изборът на последователност за методите за оптимизация, което става активно след края на случайното търсене (GAGrad.optseq).За търсенето трябва да бъдат избрани независимите променливи, както и тяхните начални стойности. След избора на последователност кликнете 'Оптимизирай!' за да стартирате процедурата.

 

 

Когато оптимизацията завърши, кликнете 'Върни'. За да видите следното:

 

 

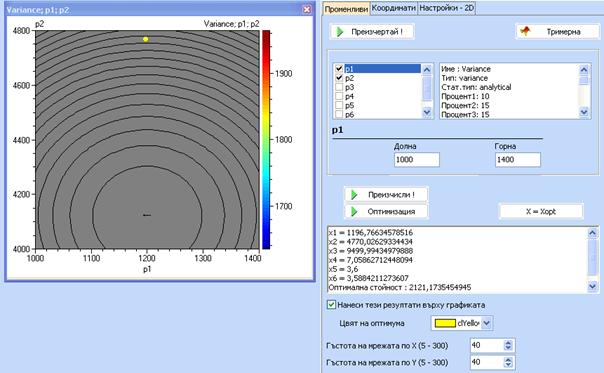
Оптималните стойности на параметрите са дадени в дясната част на екрана. Получените от Вас оптимални стойности може малко да се различават от горните поради случайният характер на търсенето. Маркирайте „Нанеси тези резултати върху графиката” за да получите оптималната точка. Трябва да се има предвид, че графиката, показана на фигурата по-горе не съответства на оптималните стойности на факторите. За да се получи графика за случая когато всички фактори са настроени на своите оптимални стойности, кликнете “X = Xopt”.. Ще получите следната графика:

 

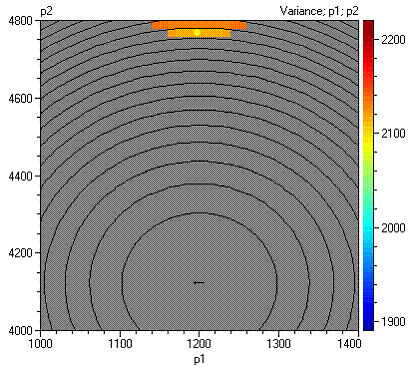
Може да се постигне по-фина граница като се увеличи гъстотата на мрежата. Фигурата по-горе е получена при гъстота на мрежата 40. Ще я изменим на 150:

Получаваме следните контури:

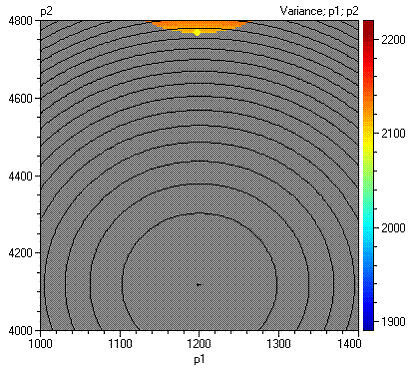
Възможно е да се начертае и тримерна графика. Кликнете   , а след това и  за да направите графиката по-фина. Получава се следното:

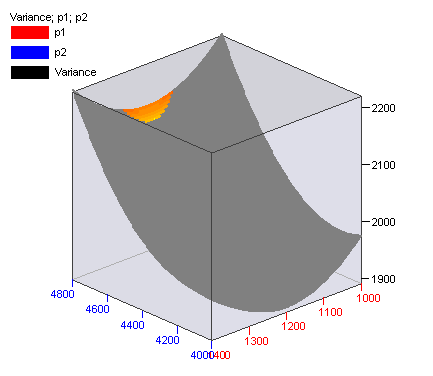
Толерансно планиране

 

Може да се направи и моделно-ориентирано толерансно планиране. Използваме същото намаляване на толерансите като Barker & Clausing за да получим сравними резултати. Толерансите се намаляват както следва:

 

SPEED: 1200  10%    (без промяна)

HTPRS: 4800   5 %    (1/3 от оригинала)

UPPRS: 9500   7.5 % (1/2 от оригинала)

LENGTH:     0   10 %  (без промяна)

HTTIME:    3.6    5 %  (1/4 от оригинала)

UPTIME:    3.6    5 %  (1/4 от оригинала)

 

С използване на моделния редактор дефинираме нови модели, означени във файла “Friction welding-Analytical-6.qsl” като Mean-T и Variance-T. Например за Mean-T дефинираме следните параметри:

 

 

Моделите за средното и дисперсията се дефинират както следва:

 

 

Сега се получават следните оптимални параметри:

 

 

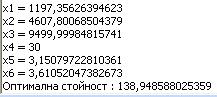
Следната фигура показва контурната диаграма за Variance-T и Mean-T след стесняването на толерансите.

 

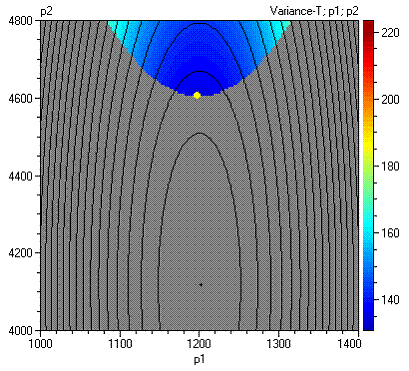
Стандартното отклонение е _, което е по-малко от полученото от Barker and Clausing (16.80). Средната якост е 160. както се изисква.

Ази графика може да бъде допълнително подобрена чрез поставяне на граница за контура средните, равен на 160 и чрез промяна на дебелината и цвета на линията както следва: 

 

 

Получава се следната графика:

 

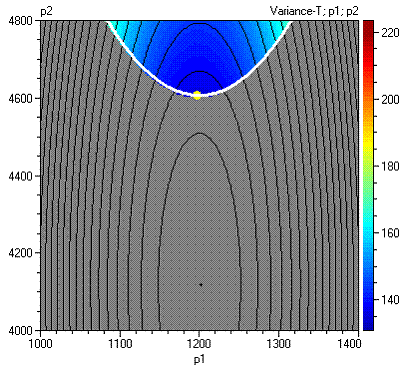
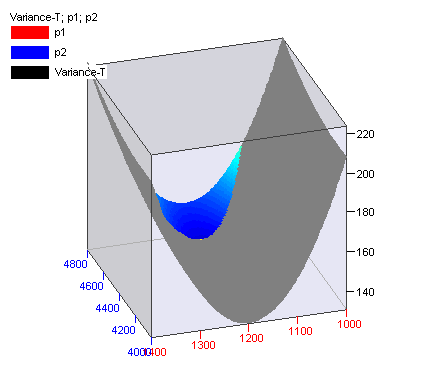
По-долу е показана и тримерната диаграма:

 

 

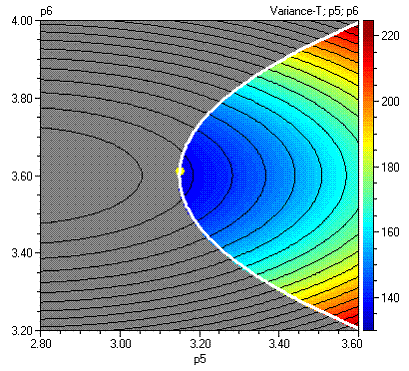
Могат да се начертаят и други контурни диаграми. Например контурната и тримерната диаграми за p5 и p6 са следните:

 

 

 

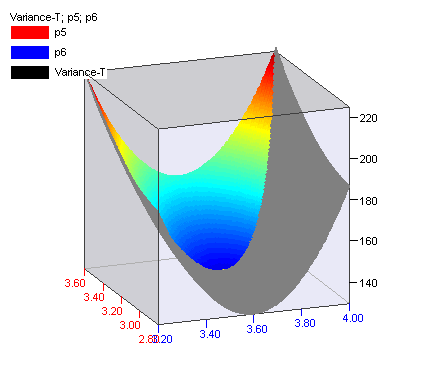
Заключение:

 

• С използването на моделен подход ние получихме резултати, които са най-малко също толкова добри, както получените по метода на Тагучи. Те са по-добри по отношение на дисперсията.
• Броят на опитите, използвани при моделно-ориентираният подход е около 20 пъти по-малък от използваните при метода на Тагучи (моделният подход използва 27 опита, методът на Тагучи – 522).
• Моделно-ориентираният подход осигурява по-добра оптимизация и графични процедури.